题目内容
15.已知a2-2a-2=0,求代数式$\frac{2}{{{a^2}-1}}÷\frac{a-1}{a+1}$的值.分析 将分母因式分解,同时将除法转化为乘法,通过约分计算分式的乘法,将分母利用完全平方公式展开,由已知可得a2-2a=2,整体代入可得.
解答 解:原式=$\frac{2}{{({a+1})({a-1})}}•\frac{a+1}{a-1}$
=$\frac{2}{{{{({a-1})}^2}}}$
=$\frac{2}{{{a^2}-2a+1}}$.
∵a2-2a-2=0,
∴a2-2a=2.
∴原式=$\frac{2}{3}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和运算法则是解题的关键,同时考查整体代入思想.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
3.对于两个不相等的示数a,b,我们规定符号Max{a,b}表示a、b中的较大值,如:Max{2,4}=4,按照这个规定,方程Max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | 1+$\sqrt{2}$或-1 | B. | 2-$\sqrt{2}$ | C. | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D. | 1-$\sqrt{2}$或-1 |
7.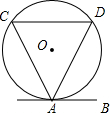 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 5 | D. | 6 |
5.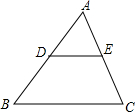 如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
 如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )
如图,点D、E分别为△ABC的边AB、AC上的中点,则△ADE的面积与四边形BCED的面积的比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:1 |
 如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.
如图,在三角形ABC中,B(2,0),把三角形ABC沿AC边平移,使A点到C点,三角形ABC变换为三角形CED,已知C(0,3.5),请写出A,D,E的坐标,并说出平移的过程.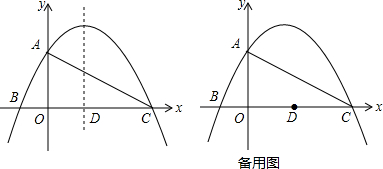
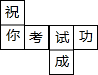 将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )
将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )