题目内容
3. 如图,在四边形ABCD中,∠A=120°,∠C=60°,AB=2,AD=DC=4,则BC边的长为6.
如图,在四边形ABCD中,∠A=120°,∠C=60°,AB=2,AD=DC=4,则BC边的长为6.
分析 连结BD,作DM⊥AB于M,DN⊥BC于N,根据三角函数可求AM=2,DM=2$\sqrt{3}$,DN=2$\sqrt{3}$,NC=2,通过HL证明Rt△BDM≌Rt△BDN,根据全等三角形的性质可得BN=BM,再根据线段的和差关系即可求解.
解答  解:连结BD,作DM⊥AB于M,DN⊥BC于N,
解:连结BD,作DM⊥AB于M,DN⊥BC于N,
∵∠BAD=120°,
∴∠MAD=180°-120°=60°,
∵AD=4,
∴AM=2,DM=2$\sqrt{3}$,
∵∠C=60°,
∴DN=2$\sqrt{3}$,NC=2,
在Rt△BDM与Rt△BDN中,
$\left\{\begin{array}{l}{DM=DN}\\{BD=BD}\end{array}\right.$,
∴Rt△BDM≌Rt△BDN(HL),
∴BN=BM=2+2=4,
∴BC=BN+NC=6.
故答案为:6.
点评 本题考查了全等三角形的判定与性质,三角函数,关键是作出辅助线,通过HL证明Rt△BDM≌Rt△BDN.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.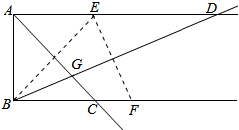 如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )
如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )
 如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )
如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )| A. | tan∠ADB=$\sqrt{2}$-1 | B. | ∠DEF=67.5° | C. | ∠AGB=∠BEF | D. | cos∠AGB=$\frac{\sqrt{6}}{4}$ |
 如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.
如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°. 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).请解答下列问题:
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).请解答下列问题: 如图,$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{2}{3}$,且△ABC的面积与△ADE的面积差是15cm2,
如图,$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{2}{3}$,且△ABC的面积与△ADE的面积差是15cm2, 如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.
如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心).下午3点时,OA与OB成直角.