题目内容
18．
如图，$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{2}{3}$，且△ABC的面积与△ADE的面积差是15cm2，（1）求证：△ADE∽△ABC；
（2）求△ADE的面积．
分析 （1）根据相似三角形的判定定理即可得到结论；
（2）由相似三角形的性质得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{2}{3}$）2=$\frac{4}{9}$，设S△ADE=4x，S△ABC=9x，根据△ABC的面积与△ADE的面积差是15cm2，列方程即可得到结论．
解答 （1）证明：∵$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{2}{3}$，∠A=∠A，
∴△ADE∽△ABC；
（2）∵△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{2}{3}$）2=$\frac{4}{9}$，
设S△ADE=4x，S△ABC=9x，
∵△ABC的面积与△ADE的面积差是15cm2，
∴9x-4x=15，
∴x=3，
∴S△ADE=4x=12cm2．
点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的性质定理是解题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：
请在同一坐标系中画出二次函数①y=$\frac{1}{2}$x2；②y=$\frac{1}{2}$（x-2）2的图象．说出两条抛物线的位置关系，指出②的开口方向、对称轴和顶点坐标及增减性．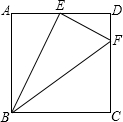
在正方形ABCD中，点E为AD中点，DF=$\frac{1}{4}$CD，则下列说法：（1）BE⊥EF；（2）图中有3对相似三角形；（3）E到BF的距离为$\frac{1}{2}$AB；（4）$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$．其中正确的有（ ）
如图，在四边形ABCD中，∠A=120°，∠C=60°，AB=2，AD=DC=4，则BC边的长为6．
