题目内容
17.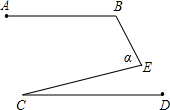 已知:AB∥CD,∠ABE=120°,∠C=25°,则∠α度数为( )
已知:AB∥CD,∠ABE=120°,∠C=25°,则∠α度数为( )| A. | 60° | B. | 75° | C. | 85° | D. | 80° |
分析 过点E作EF∥CD,根据两直线平行,同旁内角互补可得∠B+∠BEF=180°,再根据两直线平行,内错角相等得出∠C=∠FEC,然后整理即可得解.
解答 解:过E作EF∥CD,
∴∠C=∠FEC(两直线平行,内错角相等),
∴∠FEC=25°,
∵AB∥CD(已知),
∴EF∥AB(平行于同一直线的两直线平行),
∴∠B+∠BEF=180°(两直线平行,同旁内角互补),
∴∠BEF=60°,
∴∠α=∠BEF+∠FEC=85°,
故选C
点评 本题考查了平行线的判定与性质,作辅助线构造出平行线是解题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
12.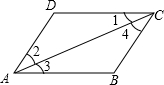 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )
 如图所示,下列推理及所注理由正确的是( )
如图所示,下列推理及所注理由正确的是( )| A. | 因为∠1=∠3,所以AB∥CD(两直线平行,内错角相等) | |
| B. | 因为AB∥CD,所以∠2=∠4(两直线平行,内错角相等) | |
| C. | 因为AD∥BC,所以∠3=∠4(两直线平行,内错角相等) | |
| D. | 因为∠2=∠4,所以AD∥BC(内错角相等,两直线平行) |
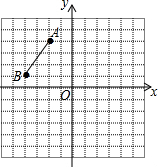 如图,在平面直角坐标系中,A(-2,4),B(-4,1),将线段AB向右平移5个单位、再向下平移1个单位得线段A1B1;将线段A1B1绕原点O旋转180°得线段A2B2,
如图,在平面直角坐标系中,A(-2,4),B(-4,1),将线段AB向右平移5个单位、再向下平移1个单位得线段A1B1;将线段A1B1绕原点O旋转180°得线段A2B2, 如图,直线AB与CD相交于点D,且∠AOC+∠BOD=140°,则∠AOD等于110°.
如图,直线AB与CD相交于点D,且∠AOC+∠BOD=140°,则∠AOD等于110°.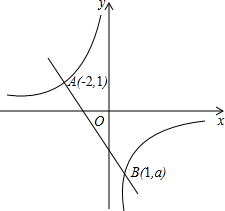 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1,n)两点.