题目内容
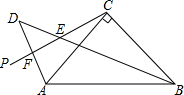 如图,△ACB是等腰直角三角形,AC=BC,做射线CP,使∠ACP=20°,点A关于CP的对称点是D,连接AD交CP于点F,连接BD交CP于点E.
如图,△ACB是等腰直角三角形,AC=BC,做射线CP,使∠ACP=20°,点A关于CP的对称点是D,连接AD交CP于点F,连接BD交CP于点E.(1)求∠CBD的度数;
(2)用等式表示线段DE、EB、AB之间的数量关系,并证明.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)连接DC,证明△DCF与△ACF全等,可得DC=AC,再得出DC=BC,△DCB是等腰三角形,得出∠CBD的度数即可;
(2)连接AE,根据线段垂直平分线,得出DE=AE,根据三角形内角和得出∠AEB=90°,再根据勾股定理得出AE、EB、AB的关系,可得DE、EB、AB的关系即可.
(2)连接AE,根据线段垂直平分线,得出DE=AE,根据三角形内角和得出∠AEB=90°,再根据勾股定理得出AE、EB、AB的关系,可得DE、EB、AB的关系即可.
解答:
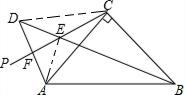 解:(1)连接DC,
解:(1)连接DC,
∵点A关于CP的对称点是D,
∴CP⊥AD,DF=AF,
∴CD=CA,∠DCP=∠PCA=20°
∵△ACB是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴DC=BC
∴∠CBD=∠CDB=
×(180°-20°-20°-90°)=25°;
(2)DE2+EB2=AB2,证明如下:
连接AE,
∵在△CDE与△CAE中,
∴△CDE≌△CAE(SAS),
∴∠EAC=∠CDB=25°,
∴∠AEB=180°-25°-45°-(45°-25°)=90°,
∴△AEB是Rt△,
∴AE2+EB2=AB2,
∵CP⊥AD,DF=AF,
∴DE=AE,
∴DE2+EB2=AB2.
 解:(1)连接DC,
解:(1)连接DC,∵点A关于CP的对称点是D,
∴CP⊥AD,DF=AF,
∴CD=CA,∠DCP=∠PCA=20°
∵△ACB是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∴DC=BC
∴∠CBD=∠CDB=
| 1 |
| 2 |
(2)DE2+EB2=AB2,证明如下:
连接AE,
∵在△CDE与△CAE中,
|
∴△CDE≌△CAE(SAS),
∴∠EAC=∠CDB=25°,
∴∠AEB=180°-25°-45°-(45°-25°)=90°,
∴△AEB是Rt△,
∴AE2+EB2=AB2,
∵CP⊥AD,DF=AF,
∴DE=AE,
∴DE2+EB2=AB2.
点评:此题考查全等三角形的判定和性质问题,注意勾股定理的应用,此题难度较大.

练习册系列答案
相关题目
在数轴上,0为原点,某点A移动到B,移动了12.6个单位长度;点A表示数a,点B表示数b,且a+b=0,A到0的距离为( )
| A、12.6 | B、6.3 |
| C、-12.6 | D、-6.3 |
 在四边形ABCD中,AD∥BC,点E为CD的中点.求证:S△AEB=
在四边形ABCD中,AD∥BC,点E为CD的中点.求证:S△AEB=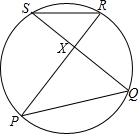 已知P、Q、R、S在圆上,PR与QS相交于X,三角形RSX的面积为1.2,PX=3SX.则三角形PQX的面积为
已知P、Q、R、S在圆上,PR与QS相交于X,三角形RSX的面积为1.2,PX=3SX.则三角形PQX的面积为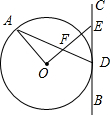 如图,已知BC与⊙O相切于点D,A为⊙O上的动点,OE⊥OA,OE分别与BC、AD交于点E、F.
如图,已知BC与⊙O相切于点D,A为⊙O上的动点,OE⊥OA,OE分别与BC、AD交于点E、F.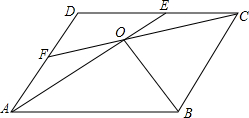 如图,在平行四边形ABCD中,AE=CF,求证:∠AOB=∠COB.
如图,在平行四边形ABCD中,AE=CF,求证:∠AOB=∠COB.