题目内容
15.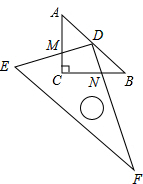 如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.
如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.(1)判断DM与DN的大小关系,并说明理由.
(2)在转动过程中,直角三角尺与△ABC重叠部分为四边形DMCN,试判断四边形DMCN的面积是否会发生变化?若变化,请说明是如何变化的;若不变化,求出其面积.
分析 (1)连接BD,求出∠MBD=∠C,∠MDB=∠CDN,BD=DC,证△BDM≌△CDN即可;
(2)求出△BDM和△CDN面积相等,求出四边形DMBN的面积等于△BDC面积,等于△ABC面积的一半,求出△ACB的面积即可.
解答 (1)相等,
证明: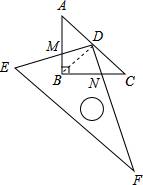 连接BD,
连接BD,
∵△ABC中,AB=BC=1,∠ABC=90°,D为AC中点,
∴BD=DC=$\frac{1}{2}$AC,∠ABD=∠CBD=∠A=∠C=45°,BD⊥AC,
∴∠BDC=90°=∠EDF,
∴∠MDB=∠CDN=90°-∠BDN,
在△BMD和△CND中,
$\left\{\begin{array}{l}{∠NBD=∠C}\\{BD=DC}\\{∠BDM=∠CDN}\end{array}\right.$,
∴△BMD≌△CND(ASA),
∴DM=DN;
(2)解:不发生变化,
∵△BMD≌△CND,
∴S△BMD=S△CND,
∴S四边形DMBN=S△BMD+S△BDN
=S△CDN+S△BDN=S△BDC
=$\frac{1}{2}$S△ACB
=$\frac{1}{2}$×$\frac{1}{2}$×1×1
=$\frac{1}{4}$.
点评 本题考查了等腰直角三角形的性质,直角三角形斜边上中线的性质,全等三角形的性质和判定的应用,连接BD构造全等三角形是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
3.将抛物线y=3x2向右平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( )
| A. | y=3(x+2)2+3 | B. | y=3(x+2)2-3 | C. | y=3(x-2)2+3 | D. | y=3(x-2)2-3 |
20.对于一组数据:3、3、2、3、6、3、10、3、6、3、2,下列说法正确的是( )
| A. | 这组数据的众数是3 | |
| B. | 这组数据的众数与中位数的数值不等 | |
| C. | 这组数据的中位数与平均数的数值相等 | |
| D. | 这组数据的平均数与众数的数值相等 |
 如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBE:∠A=1:4,则∠AED=50°.
如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBE:∠A=1:4,则∠AED=50°.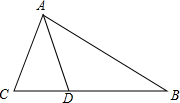 如图,△ABC中,∠BAC的角平分线交BC于D,且AB=AC+CD.
如图,△ABC中,∠BAC的角平分线交BC于D,且AB=AC+CD. 如图是正方体的展开图,则原正方体相对两个面上的数字和的最小值是6..
如图是正方体的展开图,则原正方体相对两个面上的数字和的最小值是6..