题目内容
7.函数y=$\frac{x}{\sqrt{3-5x}}$中,自变量x的取值范围是x<$\frac{3}{5}$.分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:由题意,得
3-5x>0,
解得x<$\frac{3}{5}$,
故答案为:x<$\frac{3}{5}$.
点评 本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2. 如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )
 如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )| A. | 20° | B. | 40° | C. | 60° | D. | 80° |
12.若点P(-a,a-3)关于原点对称的点是第二象限内的点,则a满足( )
| A. | a>3 | B. | 0<a≤3 | C. | a<0 | D. | a<0或a>3 |
17.已知a=2cm,b=10mm,那么$\frac{a}{b}$的值为( )
| A. | $\frac{1}{50}$ | B. | $\frac{1}{5}$ | C. | 2 | D. | $\frac{5}{2}$ |
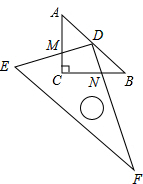 如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.
如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.