题目内容
5.已知直角三角形的两条边长分别为6和8,那么该直角三角形斜边上的中线长是4或5.分析 根据题意得出两种情况,求出斜边,即可得出答案.
解答 解:分为两种情况:当6和8都是直角边时,斜边为$\sqrt{{6}^{2}+{8}^{2}}$=10,
则该直角三角形斜边上的中线长为$\frac{1}{2}×10=5$;
当6为直角边,8为斜边时,
则此时该直角三角形斜边上的中线长是$\frac{1}{2}×8$=4;
故答案为:4或5.
点评 本题考查了勾股定理,直角三角形斜边上的中线的应用,能求出符合条件的所以情况是解此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.在△ABC中,若cosA=$\frac{\sqrt{2}}{2}$,tanB=$\sqrt{3}$,则这个三角形一定是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 锐角三角形 |
14.函数y=(m-2)x2+5x是为关于x的二次函数,其图象开口向下,则m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | m≥2 | D. | m≤2 |
 我国民间相传的正五边形的近似画法口诀是“九五顶五九,八五两边分”,它的意义如图所示.“九五顶五九”是正五边形的一条高,“八五两边分”是正五边形的一条对角线和一个底边,这三条线垂直相交,刚好是一个“士”字,把五个点连起来,刚好是一个正五边形.请你用民间相传的口诀,画一个边长为10cm的正五边形.
我国民间相传的正五边形的近似画法口诀是“九五顶五九,八五两边分”,它的意义如图所示.“九五顶五九”是正五边形的一条高,“八五两边分”是正五边形的一条对角线和一个底边,这三条线垂直相交,刚好是一个“士”字,把五个点连起来,刚好是一个正五边形.请你用民间相传的口诀,画一个边长为10cm的正五边形.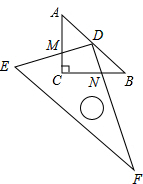 如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.
如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.