题目内容
6. 如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBE:∠A=1:4,则∠AED=50°.
如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBE:∠A=1:4,则∠AED=50°.
分析 由DE垂直平分AB,可得AE=BE,又由在△ABC中,∠C=90°,∠CBE:∠A=1:4,可设∠A=4x°,即可得方程:4x+5x=90,继而求得答案.
解答 解:∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE,
∵在△ABC中,∠C=90°,∠CBE:∠A=1:4,
设∠A=4x°,
则∠ABC=∠ABE+∠CBE=4x+x=5x°,
∴4x+5x=90,
解得:x=10,
∴∠A=40°,
∴∠AED=90°-∠A=50°.
故答案为:50°.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
相关题目
14.函数y=(m-2)x2+5x是为关于x的二次函数,其图象开口向下,则m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | m≥2 | D. | m≤2 |
 我国民间相传的正五边形的近似画法口诀是“九五顶五九,八五两边分”,它的意义如图所示.“九五顶五九”是正五边形的一条高,“八五两边分”是正五边形的一条对角线和一个底边,这三条线垂直相交,刚好是一个“士”字,把五个点连起来,刚好是一个正五边形.请你用民间相传的口诀,画一个边长为10cm的正五边形.
我国民间相传的正五边形的近似画法口诀是“九五顶五九,八五两边分”,它的意义如图所示.“九五顶五九”是正五边形的一条高,“八五两边分”是正五边形的一条对角线和一个底边,这三条线垂直相交,刚好是一个“士”字,把五个点连起来,刚好是一个正五边形.请你用民间相传的口诀,画一个边长为10cm的正五边形.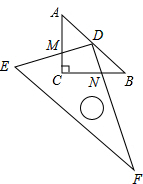 如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.
如图,在△ABC中,AC=BC=1,∠ACB=90°,把一块含30°角的直角三角尺(△DEF)的直角顶点D放在AB边的中点上,将直角三角尺绕点D转动,其中DE交AC于点M,DF交BC于点N.