题目内容
19.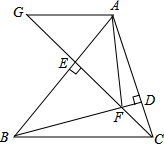 如图.在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE交于点F,∠BCE=45°
如图.在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE交于点F,∠BCE=45° (1)求证:BF=AC;
(2)延长CE到G,使CG=AB,求证:点F、G关于直线AB对称.
分析 (1)由垂直的定义得到∠BEC=∠BDC=90°,由∠BFE=∠CFD,得到∠ABD=∠ACE,推出△EBC都为等腰直角三角形,得到BE=CE,证得△BEF≌△CEA(ASA),根据全等三角形的性质即可得到结论.
(2)由CE⊥AB,得到∠AEG=90°,根据全等三角形的性质得到AE=EF,由于CG=AB,BE=CE,于是得到GE=AE,求得GE=EF,即可得到结论.
解答 证明:(1)∵BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90°,
∵∠BFE=∠CFD,
∴∠ABD=∠ACE,
∵∠BCG=45°,
∴△EBC都为等腰直角三角形,
∴BE=CE,
在△BEF和△CEA中,
$\left\{\begin{array}{l}{∠BEF=∠AEC}\\{BE=CE}\\{∠ABD=∠ACE}\end{array}\right.$,
∴△BEF≌△CEA(ASA),
∴BF=AC;
(2)∵CE⊥AB,
∴∠AEG=90°,
∵△BEF≌△CEA,
∴AE=EF,
又∵CG=AB,BE=CE,
∴GE=AE,
∴GE=EF,
又∵CE⊥AB,
∴F、G关于AB对称.
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的性质和判定,轴对称的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
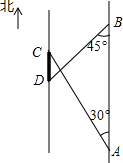 如图,一条南北走向的两岸互相平行.甲、乙二人分别站在河东岸的A、B处观察河西岸某景观建筑物.甲同学测得该建筑物一端C在A的北偏西30°方向,乙同学测得该建筑物另一端D在B的南偏西45°方向上.已知A、B点相距240米,河宽100米,求景观建筑物两端点C、D之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,一条南北走向的两岸互相平行.甲、乙二人分别站在河东岸的A、B处观察河西岸某景观建筑物.甲同学测得该建筑物一端C在A的北偏西30°方向,乙同学测得该建筑物另一端D在B的南偏西45°方向上.已知A、B点相距240米,河宽100米,求景观建筑物两端点C、D之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)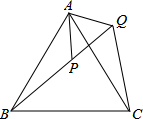 等边△ABC、等边△APQ中,点P在△ABC内,点Q在△ABC外,求证:BP=CQ.
等边△ABC、等边△APQ中,点P在△ABC内,点Q在△ABC外,求证:BP=CQ.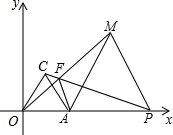 若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F.求证:AF+MF=PF.
若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F.求证:AF+MF=PF.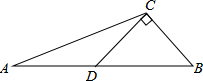 如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.
如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.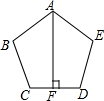 如图,正五边形ABCDE中,AF⊥CD,垂足为F
如图,正五边形ABCDE中,AF⊥CD,垂足为F