题目内容
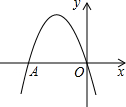 如图,二次函数y=ax2-4x+c的图象过原点,与x轴交于点A(-4,0).
如图,二次函数y=ax2-4x+c的图象过原点,与x轴交于点A(-4,0).(1)求此二次函数的解析式.
(2)在抛物线上存在点P,满足S△AOP=8,求出点P的坐标.
(3)将图中抛物线向右平移m个单位,使所得到的图象恰好与直线y=2x只有一个公共点,求m的值.
考点:待定系数法求二次函数解析式,二次函数图象与几何变换
专题:计算题
分析:(1)把原点与A坐标代入二次函数解析式求出a与c的值,即可确定出解析式;
(2)由AO的长以及三角形AOP的面积,求出P纵坐标,进而确定出横坐标即可;
(3)表示出向右平移m个单位的解析式,与y=2x联立,消去y后得到关于x的一元二次方程,根据两函数只有一个公共点得到根的判别式等于0,求出m的值即可.
(2)由AO的长以及三角形AOP的面积,求出P纵坐标,进而确定出横坐标即可;
(3)表示出向右平移m个单位的解析式,与y=2x联立,消去y后得到关于x的一元二次方程,根据两函数只有一个公共点得到根的判别式等于0,求出m的值即可.
解答:解:(1)把A(-4,0)与原点(0,0)代入得:
,
解得:a=-1,c=0,
则二次函数的解析式为y=-x2-4x;
(2)设P纵坐标为b,
∵OA=4,S△AOP=8,
∴
•OA•|b|=8,即|b|=4,
解得:b=4或-4,
当b=4时,可得-x2-4x=4,解得x=-2,
∴P(-2,4);
当b=-4时,可得-x2-4x=-4,解得x1=-2+2
,x2=-2-2
,
∴P(-2+2
,-4)或(-2-2
,-4);
(3)由题意得到平移后抛物线解析式为y=-(x+2-m)2+4,
与y=2x联立消去y得:2x=-(x+2-m)2+4,
整理得:x2+(6-2m)+m2-4m=0,
由两函数只有一个交点,得到△=0,
即(6-2m)2-4(m2-4m)=0,
解得:m=4.5.
|
解得:a=-1,c=0,
则二次函数的解析式为y=-x2-4x;
(2)设P纵坐标为b,
∵OA=4,S△AOP=8,
∴
| 1 |
| 2 |
解得:b=4或-4,
当b=4时,可得-x2-4x=4,解得x=-2,
∴P(-2,4);
当b=-4时,可得-x2-4x=-4,解得x1=-2+2
| 2 |
| 2 |
∴P(-2+2
| 2 |
| 2 |
(3)由题意得到平移后抛物线解析式为y=-(x+2-m)2+4,
与y=2x联立消去y得:2x=-(x+2-m)2+4,
整理得:x2+(6-2m)+m2-4m=0,
由两函数只有一个交点,得到△=0,
即(6-2m)2-4(m2-4m)=0,
解得:m=4.5.
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
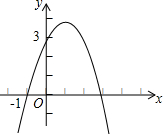 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)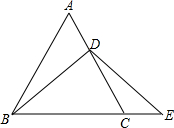 已知:△ABC是等边三角形,点D是线段AC上一点,作DB=ED,交BC延长线于点E.
已知:△ABC是等边三角形,点D是线段AC上一点,作DB=ED,交BC延长线于点E.