题目内容
在△ABC中,若|tanA-
|+(
-cosB)2=0,则∠C的度数为 .
| ||
| 3 |
| ||
| 2 |
考点:特殊角的三角函数值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:先根据非负数的性质求出tanA及cosB的值,再根据特殊角的三角函数值求出∠A及∠B的值,根据三角形内角和定理即可得出结论.
解答:解:∵|tanA-
|+(
-cosB)2=0,
∴tanA-
=0,
-cosB=0,
∴tanA=
,cosB=
,
∴∠A=30°,∠B=30°,
∴∠C=180°-30°-30°=120°.
故答案为:120°.
| ||
| 3 |
| ||
| 2 |
∴tanA-
| ||
| 3 |
| ||
| 2 |
∴tanA=
| ||
| 3 |
| ||
| 2 |
∴∠A=30°,∠B=30°,
∴∠C=180°-30°-30°=120°.
故答案为:120°.
点评:本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a-a3=a3 |
| B、(ab)3=a3b |
| C、(a3)2=a6 |
| D、a8÷a4=a2 |
已知数据:8,9,6,8,9,10,6,8,9,7.则这组数据的极差是( )
| A、10 | B、6 | C、4 | D、-4 |
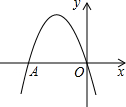 如图,二次函数y=ax2-4x+c的图象过原点,与x轴交于点A(-4,0).
如图,二次函数y=ax2-4x+c的图象过原点,与x轴交于点A(-4,0).