题目内容
在△ABC中,D是BC上的一点,∠DAC=∠B=60°,AD=
,AB=4,求AC的长度.
| 13 |
考点:正弦定理与余弦定理,相似三角形的判定与性质
专题:
分析:设BD=x,DC=y,易证△CAD∽△CBA,根据相似三角形的性质可得AC2=CD•CB=y(x+y).在△ABD中运用余弦定理可求出x的值,由于x的值有两个,故需分情况讨论,然后只需在△ABC中运用余弦定理就可求出y的值,从而求出AC的长度.
解答:解:设BD=x,DC=y,
∵∠DAC=∠B=60°,∠C=∠C,
∴△CAD∽△CBA,
∴
=
,
∴AC2=CD•CB=y(x+y).
在△ABD中,
根据余弦定理可得:
AD2=AB2+BD2-2AB•BD•cos∠B.
∵AD=
,AB=4,BD=x,∠B=60°,
∴13=16+x2-2×4x×
,
整理得:x2-4x+3=0,
解得:x1=1,x2=3.
①当BD=x=1时,如图1,
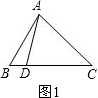
此时AC2=CD•CB=y(1+y).
在△ABC中,
根据余弦定理可得:
AC2=AB2+BC2-2AB•BC•cos∠B.
∵AC2=y(1+y),AB=4,BC=1+y,∠B=60°,
∴y(1+y)=16+(1+y)2-2×4(1+y)×
解得:y=
,
∴AC2=
×(1+
)=
,
∴AC=
.
②当BD=x=3时,如图2,

此时AC2=CD•CB=y(3+y).
在△ABC中,
根据余弦定理可得:
AC2=AB2+BC2-2AB•BC•cos∠B.
∵AC2=y(3+y),AB=4,BC=3+y,∠B=60°,
∴y(3+y)=16+(3+y)2-2×4(3+y)×
解得:y=13,
∴AC2=13×(3+13)=16×13,
∴AC=4
.
综上所述:AC的长度为
或4
.
∵∠DAC=∠B=60°,∠C=∠C,
∴△CAD∽△CBA,
∴
| CA |
| CB |
| CD |
| CA |
∴AC2=CD•CB=y(x+y).
在△ABD中,
根据余弦定理可得:
AD2=AB2+BD2-2AB•BD•cos∠B.
∵AD=
| 13 |
∴13=16+x2-2×4x×
| 1 |
| 2 |
整理得:x2-4x+3=0,
解得:x1=1,x2=3.
①当BD=x=1时,如图1,

此时AC2=CD•CB=y(1+y).
在△ABC中,
根据余弦定理可得:
AC2=AB2+BC2-2AB•BC•cos∠B.
∵AC2=y(1+y),AB=4,BC=1+y,∠B=60°,
∴y(1+y)=16+(1+y)2-2×4(1+y)×
| 1 |
| 2 |
解得:y=
| 13 |
| 3 |
∴AC2=
| 13 |
| 3 |
| 13 |
| 3 |
| 16×13 |
| 9 |
∴AC=
4
| ||
| 3 |
②当BD=x=3时,如图2,

此时AC2=CD•CB=y(3+y).
在△ABC中,
根据余弦定理可得:
AC2=AB2+BC2-2AB•BC•cos∠B.
∵AC2=y(3+y),AB=4,BC=3+y,∠B=60°,
∴y(3+y)=16+(3+y)2-2×4(3+y)×
| 1 |
| 2 |
解得:y=13,
∴AC2=13×(3+13)=16×13,
∴AC=4
| 13 |
综上所述:AC的长度为
4
| ||
| 3 |
| 13 |
点评:本题主要考查了余弦定理、相似三角形的判定与性质、解一元二次方程、解一元一次方程等知识,运用余弦定理和相似三角形的性质是解决本题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知数据:8,9,6,8,9,10,6,8,9,7.则这组数据的极差是( )
| A、10 | B、6 | C、4 | D、-4 |
在-﹙-8﹚,﹙-1﹚2011,-32,-|-1|,-|0|,-
中,负数共有( )
| 22 |
| 5 |
| A、4个 | B、3个 | C、2个 | D、1个 |
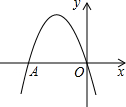 如图,二次函数y=ax2-4x+c的图象过原点,与x轴交于点A(-4,0).
如图,二次函数y=ax2-4x+c的图象过原点,与x轴交于点A(-4,0).
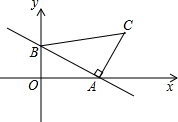 如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求过B,C两点的直线的表达式.
如图,一次函数y=-x+2的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求过B,C两点的直线的表达式.