题目内容
15.已知m=$\sqrt{3}$-1,求$\frac{2}{m+1}+\frac{{{m^2}-4m+4}}{{{m^2}-1}}÷\frac{m-2}{m-1}$的值.分析 先根据分式混合运算的法则把原式进行化简,再把m的值再代入进行计算即可.
解答 解:原式=$\frac{2}{m+1}$+$\frac{{(m-2)}^{2}}{(m+1)(m-1)}$÷$\frac{m-2}{m-1}$
=$\frac{2}{m+1}$+$\frac{m-2}{m+1}$
=$\frac{m}{m+1}$,
当m=$\sqrt{3}$-1时,原式=$\frac{m}{m+1}$=$\frac{\sqrt{3}-1}{\sqrt{3}}$=1-$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
6.中国国家图书馆是亚洲最大的图书馆,截止到今年初馆藏图书达3119万册,其中古籍善本约有2000000册.2000000用科学记数法可以表示为( )
| A. | 0.2×107 | B. | 2×106 | C. | 20×105 | D. | 10×26 |
20. 如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
 如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )
如图,AB∥CD,AC的垂直平分线交CD于点F,交AC于点E,连接AF,若∠BAF=80°,则∠C的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
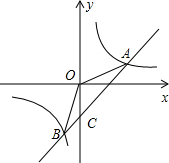 如图,已知一次函数y=kx+b的图象和反比例函数$y=\frac{3}{x}$的图象相交于A(3,m),B(n,-3)两点
如图,已知一次函数y=kx+b的图象和反比例函数$y=\frac{3}{x}$的图象相交于A(3,m),B(n,-3)两点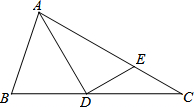 已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2.
已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2.