题目内容
3.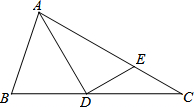 已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2.
已知,△ABC中,D是BC上的一点,且∠DAC=30°,过点D作ED⊥AD交AC于点E,AE=4,EC=2.(1)求证:AD=CD;
(2)若tanB=3,求线段AB的长.
分析 (1)先由ED⊥AD,得出∠ADE=90°.解Rt△ADE,求出∠DEA=60°,DE=$\frac{1}{2}$AE=2,由EC=2,得到DE=EC,那么∠EDC=∠C,根据三角形外角的性质得出∠EDC+∠C=∠DEA=60°,那么求出∠C=30°=∠DAE,根据等角对等边得出AD=DC;
(2)过点A作AF⊥BC于点F,则∠AFC=∠AFB=90°,AC=AE+EC=6.解Rt△AFC,得出AF=$\frac{1}{2}$AC=3.再解Rt△AFB,利用三角函数定义求出BF=$\frac{AF}{tanB}$=1,再根据勾股定理即可求出AB.
解答 (1)证明:∵ED⊥AD,
∴∠ADE=90°.
在Rt△ADE中,∠DAE=30°,AE=4,
∴∠DEA=60°,DE=$\frac{1}{2}$AE=2,
∵EC=2,
∴DE=EC,
∴∠EDC=∠C.
又∵∠EDC+∠C=∠DEA=60°,
∴∠C=30°=∠DAE,
∴AD=CD;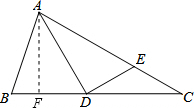 (2)解:如图,过点A作AF⊥BC于点F,则∠AFC=∠AFB=90°.
(2)解:如图,过点A作AF⊥BC于点F,则∠AFC=∠AFB=90°.
∵AE=4,EC=2,
∴AC=6.
在Rt△AFC中,∠AFC=90°,∠C=30°,
∴AF=$\frac{1}{2}$AC=3.
在Rt△AFB中,∠AFB=90°,tanB=3,
∴BF=$\frac{AF}{tanB}$=1,
∴AB=$\sqrt{A{F}^{2}+B{F}^{2}}$=$\sqrt{10}$.
点评 本题考查了解直角三角形,等腰三角形的判定与性质,三角形外角的性质,三角函数定义,勾股定理,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根0,则a值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
11.在学习“用直尺和圆规作一个角等于已知角”时,教科书介绍如图:对于“想一想”中的问题,下列回答正确的是( )


| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |
8.甲、乙两人进行射击比赛,他们5次射击的成绩(单位:环)如图所示:设甲、乙两人射击成绩的平均数依次为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,射击成绩的方差依次为$S_甲^2$、$S_乙^2$,那么下列判断中正确的是( )
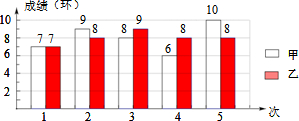

| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2=S_乙^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2>S_乙^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ |
12.-$\frac{2}{5}$的倒数是( )
| A. | -$\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
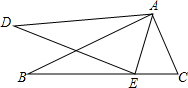 如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB
如图,在△ABC和△ADE中,点E在BC上,∠B=∠D,AB=AD,∠EAC=∠DAB