题目内容
17. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度i=1:$\sqrt{3}$的新传送带AC(如图所示).已知原传送带AB的长是4$\sqrt{2}$米.那么新传送带AC的长是8米.
某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角为45°的传送带AB,调整为坡度i=1:$\sqrt{3}$的新传送带AC(如图所示).已知原传送带AB的长是4$\sqrt{2}$米.那么新传送带AC的长是8米.
分析 根据题意首先得出AD,BD的长,再利用坡角的定义得出DC的长,再结合勾股定理得出答案.
解答  解:过点A作AD⊥CB延长线于点D,
解:过点A作AD⊥CB延长线于点D,
∵∠ABD=45°,
∴AD=BD,
∵AB=4$\sqrt{2}$,
∴AD=BD=ABsin45°=4$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=4,
∵坡度i=1:$\sqrt{3}$,
∴$\frac{AD}{DC}$=$\frac{4}{DC}$=$\frac{1}{\sqrt{3}}$,
则DC=4$\sqrt{3}$,
故AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=8(m).
故答案为:8.
点评 此题主要考查了勾股定理以及解直角三角形的应用等知识,正确得出DC,AD的长是解题关键.

练习册系列答案
相关题目
 如图,按要求画图:
如图,按要求画图: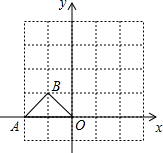 如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′.
如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′.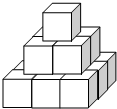 如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g.
如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g. 如图,△ABC中,AB=AC,AE是外角∠CAD的平分线,点F在AC上,连结BF并延长与AE交于点E.
如图,△ABC中,AB=AC,AE是外角∠CAD的平分线,点F在AC上,连结BF并延长与AE交于点E.  如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证:
如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂直分布为E、F,连接EF交AB于点M,交AC于点N,求证: 如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.
如图,已知平行四边形ABCD中,AB=2$\sqrt{5}$,AD=6,cot∠ABC=$\frac{1}{2}$,将边AB绕点A旋转,使得点B落在平行四边形ABCD的边上,其对应点为B′(点B′不与点B重合),那么sin∠CAB′=$\frac{\sqrt{10}}{10}$或$\frac{\sqrt{2}}{2}$.