题目内容
14. 如图,已知△ABC中,AB=AC,CE=BD,求证:GE=GD.
如图,已知△ABC中,AB=AC,CE=BD,求证:GE=GD.
分析 过E作EF∥AB交BC延长线于F,根据等腰三角形的性质及平行线的性质可推出∠F=∠FCE,从而可得到BD=CE=EF,再根据AAS判定△DGB≌△EGF,根据全等三角形的性质即可证得结论.
解答 证明:过E作EF∥AB交BC延长线于F.
∵AB=AC,
∴∠B=∠ACB,
∵EF∥AB,
∴∠F=∠B,
∵∠ACB=∠FCE,
∴∠F=∠FCE,
∴CE=EF,
∵BD=CE,
∴BD=EF,
在△DBG与△GEF中,
$\left\{\begin{array}{l}{∠DGB=∠EGF}\\{∠B=∠F}\\{BD=EF}\end{array}\right.$,
∴△DGB≌△EGF(AAS),
∴GD=GE.
点评 本题主要考查等腰三角形的性质及全等三角形的判定与性质的综合运用,作辅助线构造全等三角形是解决问题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
6.多项式2x2y2-3xy2+$\frac{3}{4}$的次数和项数分别是( )
| A. | 5,3 | B. | 5,2 | C. | 2,3 | D. | 4,3 |
3.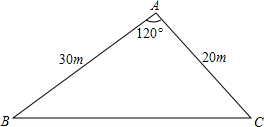 如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )
如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )
 如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )
如图,有一块三角形空地需要开发,根据图中数据可知该空地的面积为( )| A. | 100$\sqrt{3}m$2 | B. | 150$\sqrt{3}m$2 | C. | 200$\sqrt{3}m$2 | D. | 300$\sqrt{3}m$2 |
 已知关于x的不等式x>$\frac{a-3}{2}$表示在数轴上如图所示,求a的值.
已知关于x的不等式x>$\frac{a-3}{2}$表示在数轴上如图所示,求a的值.