题目内容
15.请你先将代数式$\frac{2015a}{{a}^{2}-2a+1}$÷(1-$\frac{1}{1-a}$)化简,然后从0、1、2中选择一个数作为a的值,并求出式子的值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a=2代入计算即可求出值.
解答 解:原式=$\frac{2015a}{(a-1)^{2}}$÷$\frac{1-a-1}{1-a}$
=$\frac{2015a}{(a-1)^{2}}$÷$\frac{a}{a-1}$
=$\frac{2015a}{(a-1)^{2}}$•$\frac{a-1}{a}$
=$\frac{2015}{a-1}$,
当a=2时,原式=2015.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3. 如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )
如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )
 如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )
如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )| A. | 14,15 | B. | 15,16 | C. | 15,15 | D. | 15,15.5 |

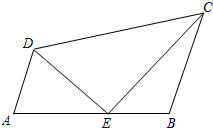 如图,已知点E在四边形ABCD的边AB上,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$.
如图,已知点E在四边形ABCD的边AB上,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$.



 如图,在直角三角形ABC中,斜边上的中线CD=AC,则∠B等于30°.
如图,在直角三角形ABC中,斜边上的中线CD=AC,则∠B等于30°.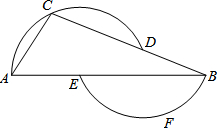 如图,点D、E在△ABC的边BC、AB上,过A、C、D三点的圆的圆心为E,过B、F、E三点的圆的圆心为D,如果∠A=57°,那么∠B=22度.
如图,点D、E在△ABC的边BC、AB上,过A、C、D三点的圆的圆心为E,过B、F、E三点的圆的圆心为D,如果∠A=57°,那么∠B=22度.