题目内容
10.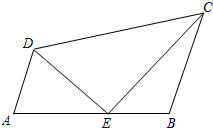 如图,已知点E在四边形ABCD的边AB上,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$.
如图,已知点E在四边形ABCD的边AB上,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$.(1)试用向量$\overrightarrow a$、$\overrightarrow b$和$\overrightarrow c$表示向量$\overrightarrow{DE}$,$\overrightarrow{EC}$;
(2)在图中求作:$\overrightarrow{DE}$+$\overrightarrow{EC}$-$\overrightarrow{DA}$.(不要求写出作法,只需写出结论即可)
分析 (1)由$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,直接利用三角形法则求解,即可求得答案;
(2)由三角形法则可得:$\overrightarrow{DE}$+$\overrightarrow{EC}$-$\overrightarrow{DA}$=$\overrightarrow{DC}$-$\overrightarrow{DA}$=$\overrightarrow{AC}$,继而可求得答案.
解答  解:(1)∵$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,
解:(1)∵$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,
∴$\overrightarrow{DE}$=$\overrightarrow{AE}$-$\overrightarrow{AD}$=$\overrightarrow{a}$-$\overrightarrow{b}$;$\overrightarrow{EC}$=$\overrightarrow{DC}$-$\overrightarrow{DE}$=$\overrightarrow{c}$-($\overrightarrow{a}$-$\overrightarrow{b}$)=$\overrightarrow{c}$-$\overrightarrow{a}$+$\overrightarrow{b}$;
(2)$\overrightarrow{DE}$+$\overrightarrow{EC}$-$\overrightarrow{DA}$=$\overrightarrow{DC}$-$\overrightarrow{DA}$=$\overrightarrow{AC}$.
如图:$\overrightarrow{AC}$即为所求.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用.

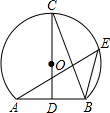 如图,点E是$\widehat{ACB}$上一动点,点D是弦AB的中点,CD经过圆心O,则下列结论中不一定正确的是( )
如图,点E是$\widehat{ACB}$上一动点,点D是弦AB的中点,CD经过圆心O,则下列结论中不一定正确的是( )| A. | CD⊥AB | B. | ∠AEB=2∠BCD | C. | ∠BAE<∠CBE | D. | $\widehat{AC}$=$\widehat{BC}$ |
| A. | 如果∠1+∠2+∠3=180°,那么∠1、∠2与∠3互为补角 | |
| B. | 如果两个角相等,那么它们的余角也相等 | |
| C. | 有公共顶点且又相等的角是对顶角 | |
| D. | 直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离 |
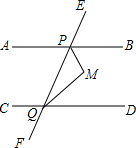 如图,直线EF与直线AB,CD分别相交于点P,Q,∠EPB=x°,∠CQP=180°-x°,PM平分∠BPQ,QM平分∠PQD,判断PM与QM之间的位置关系,并说明理由.
如图,直线EF与直线AB,CD分别相交于点P,Q,∠EPB=x°,∠CQP=180°-x°,PM平分∠BPQ,QM平分∠PQD,判断PM与QM之间的位置关系,并说明理由. 如图,在半径为5$\sqrt{2}$的⊙O中,弦AB、CD互相垂直,若AB=14,CD=10,则BC的长为6$\sqrt{5}$.
如图,在半径为5$\sqrt{2}$的⊙O中,弦AB、CD互相垂直,若AB=14,CD=10,则BC的长为6$\sqrt{5}$.