题目内容
5.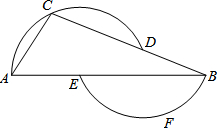 如图,点D、E在△ABC的边BC、AB上,过A、C、D三点的圆的圆心为E,过B、F、E三点的圆的圆心为D,如果∠A=57°,那么∠B=22度.
如图,点D、E在△ABC的边BC、AB上,过A、C、D三点的圆的圆心为E,过B、F、E三点的圆的圆心为D,如果∠A=57°,那么∠B=22度.
分析 连接EC、ED,如图,设∠B=x,根据等腰三角形的性质由EA=EC得∠A=∠ACE,再根据三角形内角和定理得到∠4=180°-2∠A=66°,而DB=DE,则∠1=∠B=x,利用三角形外角性质得∠2=∠1+∠B=2x,再利用EC=ED得到∠3=∠2=2x,然后根据三角形外角性质得到2x+x=66°,即得x=22°.
解答 解:连接EC、ED,如图,设∠B=x,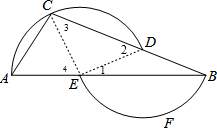
∵EA=EC,
∴∠A=∠ACE,
∴∠4=180°-2∠A=180°-2×57°=66°,
∵DB=DE,
∴∠1=∠B=x,
∴∠2=∠1+∠B=2x,
而EC=ED,
∴∠3=∠2=2x,
∵∠4=∠3+∠B,
∴2x+x=66°,即得x=22°,
即∠B=22°.
故答案为22.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
16.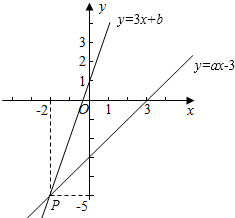 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )
如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )
 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )
如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是( )| A. | x>-2 | B. | x<-2 | C. | -2<x<0 | D. | x>0 |
10. 如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
 如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )| A. | 50° | B. | 59° | C. | 60° | D. | 62° |
17.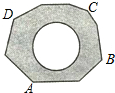 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
(1)当投掷的次数很大时,则m:n的值越来越接近0.5;
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在$\frac{1}{3}$;
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是3π米2(结果保留π)
 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下: | 50 | 50 | 300 | … |
| 石子落在圆内(含圆上)次数m | 14 | 48 | 89 | … |
| 石子落在圆以外的阴影部分(含外缘上)次数n | 30 | 95 | 180 | … |
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在$\frac{1}{3}$;
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是3π米2(结果保留π)
14.在△ABC中,AB=2,AC=3,$\overrightarrow{AB}$•$\overrightarrow{BC}$=1,则BC=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{23}$ |