题目内容
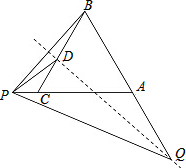 如图,等边△ABC,AB=4,点P是射线AC上的一动点,联结BP,作BP的垂直平分线交线段BD于点D,交射线BA于点Q,分别联结PD,PQ.
如图,等边△ABC,AB=4,点P是射线AC上的一动点,联结BP,作BP的垂直平分线交线段BD于点D,交射线BA于点Q,分别联结PD,PQ.(1)当点P在线段AC的延长线上时,
①求∠DPQ的度数,并求证:△DCP∽△PAQ;
②设CP=x,AQ=y,求y关于x的函数解析式,并写出它的定义域;
(2)如果△PCD是等腰三角形,求△APQ的面积.
考点:相似形综合题,三角形的外角性质,全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质
专题:综合题
分析:(1)①根据线段垂直平分线的性质可得BD=PD,BQ=PQ,即可证到△BDQ≌△PDQ,从而有∠DPQ=∠DBQ=60°;易证∠APQ=∠CDP,∠DCP=∠QAP,就可证到△DCP∽△PAQ;
②利用△DCP∽△PAQ可求出CD、BD(用x、y的代数式表示),然后根据CD+BD=BC=4就可得到y关于x的函数解析式,然后根据x、y均为正数可求出x的范围;
(2)①当点P在AC的延长线上时,∠DCP=120°,由△PCD是等腰三角形,可得CP=CD,由此可得到y=x+4,把它代入函数关系式,就可求出x的值,从而可求出CP、AP、AQ的值,就可求出△APQ的面积;②当点P在线段AC上时,∠C=60°,由△PCD是等腰三角形可得△PCD是等边三角形,从而有∠BDP=120°,进而可求出
∠DPB=30°,∠BPC=90°,根据等腰三角形的性质可得AP=CP=2.由△DCP∽△PAQ,△PCD是等边三角形可得△APQ也是等边三角形,就可求出△APQ的面积.
②利用△DCP∽△PAQ可求出CD、BD(用x、y的代数式表示),然后根据CD+BD=BC=4就可得到y关于x的函数解析式,然后根据x、y均为正数可求出x的范围;
(2)①当点P在AC的延长线上时,∠DCP=120°,由△PCD是等腰三角形,可得CP=CD,由此可得到y=x+4,把它代入函数关系式,就可求出x的值,从而可求出CP、AP、AQ的值,就可求出△APQ的面积;②当点P在线段AC上时,∠C=60°,由△PCD是等腰三角形可得△PCD是等边三角形,从而有∠BDP=120°,进而可求出
∠DPB=30°,∠BPC=90°,根据等腰三角形的性质可得AP=CP=2.由△DCP∽△PAQ,△PCD是等边三角形可得△APQ也是等边三角形,就可求出△APQ的面积.
解答:解:(1)①如图1,
∵DQ是线段BP的中垂线,
∴BD=PD,BQ=PQ.
在△BDQ和△PDQ中,
,
∴△BDQ≌△PDQ(SSS),
∴∠DPQ=∠DBQ=60°,
∴∠CPD+∠APQ=60°.
又∵∠ACB=∠CDP+∠CPD=60°,
∴∠APQ=∠CDP.
又∵∠DCP=∠QAP=120°,
∴△DCP∽△PAQ;
②∵△DCP∽△PAQ,
∴
=
=
,
∴
=
=
,
∴CD=
,BD=
,
∵BC=BD+CD=4,
∴
+
=4,
整理得:y=
.
∵x>0,y>0,∴0<x<4.
∴y关于x的函数解析式为y=
,它的定义域为0<x<4;
(2)①当点P在线段AC的延长线上时,∠DCP=120°.
∴当△PCD是等腰三角形时,CD=CP,
∴
=x,
∴y=x+4,
∴
=x+4,
解得:x1=-2-2
(舍去),x2=-2+2
,
∴CP=-2+2
,
∴AQ=AP=AC+CP=4-2+2
=2+2
.
过点Q作QH⊥AP,交PA的延长线于点H,如图2,
∴S△APQ=
AP•QH=
AP•AQ•sin∠HAQ
=
×(2+2
)2×
=4
+6;
②当点P在线段AC上时,∠C=60°,
∴当△PCD是等腰三角形时,△PCD是等边三角形,
∴∠BDP=120°.
又∵BD=DP,
∴∠DBP=∠DPB=30°,
∴∠BPC=90°,即BP⊥AC.
∵BC=BA,
∴AP=CP=2.
∵△DCP∽△PAQ,△PCD是等边三角形,
∴△APQ是等边三角形,
∴AP=AQ.
过点Q作QH⊥AP于H,如图3,
∴S△APQ═
AP•QH=
AP•AQ•sin∠HAQ=
×2×2×
=
.
∵DQ是线段BP的中垂线,

∴BD=PD,BQ=PQ.
在△BDQ和△PDQ中,
|
∴△BDQ≌△PDQ(SSS),
∴∠DPQ=∠DBQ=60°,
∴∠CPD+∠APQ=60°.
又∵∠ACB=∠CDP+∠CPD=60°,
∴∠APQ=∠CDP.
又∵∠DCP=∠QAP=120°,
∴△DCP∽△PAQ;
②∵△DCP∽△PAQ,
∴
| CD |
| AP |
| CP |
| AQ |
| DP |
| PQ |
∴
| CD |
| x+4 |
| x |
| y |
| BD |
| 4+y |
∴CD=
| x2+4x |
| y |
| 4x+xy |
| y |
∵BC=BD+CD=4,
∴
| 4x+xy |
| y |
| x2+4x |
| y |
整理得:y=
| x2+8x |
| 4-x |
∵x>0,y>0,∴0<x<4.
∴y关于x的函数解析式为y=
| x2+8x |
| 4-x |
(2)①当点P在线段AC的延长线上时,∠DCP=120°.
∴当△PCD是等腰三角形时,CD=CP,

∴
| x2+4x |
| y |
∴y=x+4,
∴
| x2+8x |
| 4-x |
解得:x1=-2-2
| 3 |
| 3 |
∴CP=-2+2
| 3 |
∴AQ=AP=AC+CP=4-2+2
| 3 |
| 3 |
过点Q作QH⊥AP,交PA的延长线于点H,如图2,
∴S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
②当点P在线段AC上时,∠C=60°,
∴当△PCD是等腰三角形时,△PCD是等边三角形,
∴∠BDP=120°.
又∵BD=DP,

∴∠DBP=∠DPB=30°,
∴∠BPC=90°,即BP⊥AC.
∵BC=BA,
∴AP=CP=2.
∵△DCP∽△PAQ,△PCD是等边三角形,
∴△APQ是等边三角形,
∴AP=AQ.
过点Q作QH⊥AP于H,如图3,
∴S△APQ═
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题主要考查了相似三角形的判定与性质、线段垂直平分线的性质、全等三角形的判定与性质、等腰三角形的性质、等边三角形的性质等知识,运用(1)中结论求出CD、BD(用x、y的代数式表示),并利用CD+BD=BC=4建立等式是解决第(2)小题的关键,运用分类讨论的思想是解决第(3)小题的关键.

练习册系列答案
相关题目
 如图,将边长为2的正方形ABCD的各边四等分,把一长度为
如图,将边长为2的正方形ABCD的各边四等分,把一长度为| 34 |
| A、CR3 |
| B、R1D |
| C、R2R3 |
| D、R2R1 |
已知点P(2,2a-3)在第一象限,则a的取值范围是( )
| A、a<-1 | ||
B、-1<a<
| ||
C、-
| ||
D、a>
|
下列说法中,正确的是( )
| A、任何数的平方根都有2个 |
| B、一个正数的平方根的平方就是它本身 |
| C、只有正数才有平方根 |
| D、-3不是9的平方根 |
已知△ABC中,∠ABC和∠ACB的平分线交于点O,则∠BOC一定( )
| A、小于直角 | B、等于直角 |
| C、大于直角 | D、不能确定 |
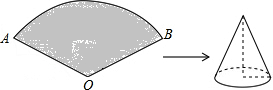 如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为
如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的全面积为