题目内容
已知△ABC中,∠ABC和∠ACB的平分线交于点O,则∠BOC一定( )
| A、小于直角 | B、等于直角 |
| C、大于直角 | D、不能确定 |
考点:三角形内角和定理,三角形的角平分线、中线和高
专题:
分析:先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠OBC+∠OCB的度数,由三角形内角和定理即可得出结论.
解答:解:在△ABC中,
∠ABC+∠ACB=180°-∠A,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×(180°-∠A)=90°-
∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-
∠A)=90°+
∠A>90°.
故选:C.
∠ABC+∠ACB=180°-∠A,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题考查的是三角形内角和定理以及角平分线的性质,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列等式从左到右变形,属于因式分解的是( )
| A、a(x-y)=ax-ay | ||
| B、x2+2x-1=x(x+2)-1 | ||
| C、a2-a=a(a-1) | ||
D、a2-1=a(a-
|
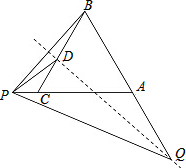 如图,等边△ABC,AB=4,点P是射线AC上的一动点,联结BP,作BP的垂直平分线交线段BD于点D,交射线BA于点Q,分别联结PD,PQ.
如图,等边△ABC,AB=4,点P是射线AC上的一动点,联结BP,作BP的垂直平分线交线段BD于点D,交射线BA于点Q,分别联结PD,PQ.
 在直角三角形ABC中,∠C=90°,BC=12cm,S△ABC=30cm2,求AB的长.
在直角三角形ABC中,∠C=90°,BC=12cm,S△ABC=30cm2,求AB的长.