题目内容
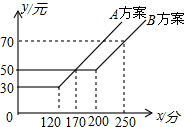 某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题:
某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题:(1)某人若按A方案通话时间为150分钟时通讯费用为
(2)求B方案的通讯费用y(元)与通话时间x(分)之间的函数关系式;
(3)当B方案的通讯费用为50元,通话时间为170分钟时,若两种方案的通讯费用相差10元,求通话时间相差多少分钟.
考点:一次函数的应用
专题:
分析:由图象获取相关信息后解答.
(1)先由图象可知若按A方案通话时间为150分钟时,通讯费与通话时间之间是一次函数关系,故先利用待定系数法求出解析式,再将x=150代入即可;通讯费为60元时B方案通讯费与通话时间之间是一次函数关系,利用待定系数法求出解析式,把y=60分别代入两个解析式即可求得通话时间,再相减即可;(2)由图象知当x≤200时,通讯费y=50元;当x≥200时,通讯费y与x是一次函数关系,利用待定系数法求出解析式即可;
(3)分两种情况:A种方案通讯费为40元时;A种方案通讯费为60元时,分别把y=40,y=60代入A方案的解析式求出通话时间,即可解答.
(1)先由图象可知若按A方案通话时间为150分钟时,通讯费与通话时间之间是一次函数关系,故先利用待定系数法求出解析式,再将x=150代入即可;通讯费为60元时B方案通讯费与通话时间之间是一次函数关系,利用待定系数法求出解析式,把y=60分别代入两个解析式即可求得通话时间,再相减即可;(2)由图象知当x≤200时,通讯费y=50元;当x≥200时,通讯费y与x是一次函数关系,利用待定系数法求出解析式即可;
(3)分两种情况:A种方案通讯费为40元时;A种方案通讯费为60元时,分别把y=40,y=60代入A方案的解析式求出通话时间,即可解答.
解答:解:(1)42,30;
(2)由图象知:当x≤200时,通讯费y=50元;
当x≥200时,设B方案的通讯费用y(元)与通话时间x(分)之间的函数关系式为y=kx+b,
把x=200,y=50;x=250,y=70代入,得
,解得,
∴当x≥200时,设B方案的通讯费用y(元)与通话时间x(分)之间的函数关系式为:y=
x-30;
(3)当x≥120时,A方案通讯费y与通话时间x之间是一次函数关系,
设此时的通讯费用y(元)与通话时间x(分)之间的函数关系式为:y=mx+n
把x=120,y=30;x=170,y=50代入,得
,解得
∴当x≥120时,通讯费用y(元)与通话时间x(分)之间的函数关系式为:y=
x-18,
当B方案的通讯费用为50元,两种方案的通讯费用相差10元,则A方案的通讯费可以是y=60元,y=40元,
把y=60代入y=
x-18,得x=195,所以通话时间相差195-170=25(分);
把y=40代入y=
x-18,得x=145,所以通话时间相差170-145=25(分);
故当B方案的通讯费用为50元,通话时间为170分钟时,若两种方案的通讯费用相差10元,求通话时间相差25分钟.
(2)由图象知:当x≤200时,通讯费y=50元;
当x≥200时,设B方案的通讯费用y(元)与通话时间x(分)之间的函数关系式为y=kx+b,
把x=200,y=50;x=250,y=70代入,得
|
|
∴当x≥200时,设B方案的通讯费用y(元)与通话时间x(分)之间的函数关系式为:y=
| 2 |
| 5 |
(3)当x≥120时,A方案通讯费y与通话时间x之间是一次函数关系,
设此时的通讯费用y(元)与通话时间x(分)之间的函数关系式为:y=mx+n
把x=120,y=30;x=170,y=50代入,得
|
|
∴当x≥120时,通讯费用y(元)与通话时间x(分)之间的函数关系式为:y=
| 2 |
| 5 |
当B方案的通讯费用为50元,两种方案的通讯费用相差10元,则A方案的通讯费可以是y=60元,y=40元,
把y=60代入y=
| 2 |
| 5 |
把y=40代入y=
| 2 |
| 5 |
故当B方案的通讯费用为50元,通话时间为170分钟时,若两种方案的通讯费用相差10元,求通话时间相差25分钟.
点评:本题主要考查一次函数的应用,是利用一次函数解决通话时间x(分)与相应的话费y(元)之间的关系,正确利用待定系数法求得函数解析式是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
若代数式
比
的值多1,则a的倒数是( )
| a+3 |
| 4 |
| 2a-3 |
| 7 |
A、
| ||
B、-
| ||
| C、5 | ||
| D、-5 |
 如图,要测量池塘两端A,B的距离,先在平面上取一个可以直接到达A,B的点C,连接AC并延长到D,使AC=3CD,连接BC并延长到E,使BC=3CE,连接DE,测得DE=13m,那么池塘的宽AB是多少?
如图,要测量池塘两端A,B的距离,先在平面上取一个可以直接到达A,B的点C,连接AC并延长到D,使AC=3CD,连接BC并延长到E,使BC=3CE,连接DE,测得DE=13m,那么池塘的宽AB是多少?下列去括号中,正确的是( )
| A、-(x-y+z)=-x+y-z | ||||||
| B、x+2(y-z)=x+2y-z | ||||||
C、a2-
| ||||||
| D、a-(x-y+z)=a-x+y+z |
 已知:如图,数轴上A、B、C、D四点对应的分别是整数a、b、c、d,且有a+2b+c-d=-1,那么,原点应是点( )
已知:如图,数轴上A、B、C、D四点对应的分别是整数a、b、c、d,且有a+2b+c-d=-1,那么,原点应是点( ) 如图,∠AGF=∠EHC,∠B=∠D,求证:AD∥BC.
如图,∠AGF=∠EHC,∠B=∠D,求证:AD∥BC.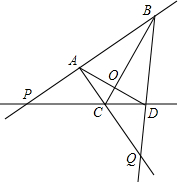 如图,已知A、B、C、D四个点.
如图,已知A、B、C、D四个点.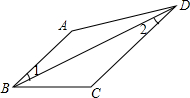 如图,在四边形ABCD中,∠A=130°,∠ADC=50°,试说明∠1=∠2.
如图,在四边形ABCD中,∠A=130°,∠ADC=50°,试说明∠1=∠2.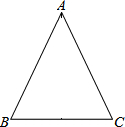 在△ABC中,AB=AC=17,BC=16,求S△ABC.
在△ABC中,AB=AC=17,BC=16,求S△ABC.