题目内容
 如图,∠AGF=∠EHC,∠B=∠D,求证:AD∥BC.
如图,∠AGF=∠EHC,∠B=∠D,求证:AD∥BC.考点:平行线的判定与性质
专题:证明题
分析:由∠AGF=∠EHC和对顶角相等可证明BF∥DE,由平行线的性质结合条件可证明∠B+∠BFD=180°,可证得AD∥BC.
解答:证明:
∵∠AGF=∠EHC,且∠EHC=∠AHD,
∴∠AGF=∠AHD,
∴BF∥DE,
∴∠D+∠BFD=180°,
又∠B=∠D,
∴∠B+∠BFD=180°,
∴AD∥BC.
∵∠AGF=∠EHC,且∠EHC=∠AHD,
∴∠AGF=∠AHD,
∴BF∥DE,
∴∠D+∠BFD=180°,
又∠B=∠D,
∴∠B+∠BFD=180°,
∴AD∥BC.
点评:本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
下列事件属于随机事件的是( )
| A、任意画一个三角形,其内角和是180° |
| B、掷一次骰子,向上的一面的点数是7 |
| C、从只有红球的袋子中,摸出1个白球 |
| D、打开电视,电视正在播放新闻节目 |
 如图所示,一条钢丝绳固定杆BC,钢丝绳与地面夹角为30°,BC高18米,则钢丝绳AC的长为( )
如图所示,一条钢丝绳固定杆BC,钢丝绳与地面夹角为30°,BC高18米,则钢丝绳AC的长为( )| A、9米 | B、18米 |
| C、27米 | D、36米 |
设某数是x,若比它的2倍大3的数是8,可列方程为( )
| A、2x-3=8 | ||
| B、2x+3=8 | ||
C、
| ||
D、
|
 如图所示,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,它的左视图是( )
如图所示,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,它的左视图是( )



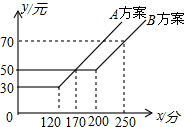 某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题:
某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题: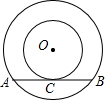 半径为5的大⊙O的弦与小⊙O相切于点C,且AB=8,则小⊙O的半径为
半径为5的大⊙O的弦与小⊙O相切于点C,且AB=8,则小⊙O的半径为