题目内容
如果:(x+m)2=x2+kx+
,那么m= ,k= .
| 1 |
| 4 |
考点:完全平方公式
专题:
分析:先根据完全平方公式展开,即可得出2mx=kx,m2=
,求出即可.
| 1 |
| 4 |
解答:解:∵(x+m)2=x2+kx+
,
∴x2+2mx+m2=x2+kx+
,
∴2mx=kx,m2=
,
∴m=±
,k=±1,
故答案为:±
,±1.
| 1 |
| 4 |
∴x2+2mx+m2=x2+kx+
| 1 |
| 4 |
∴2mx=kx,m2=
| 1 |
| 4 |
∴m=±
| 1 |
| 2 |
故答案为:±
| 1 |
| 2 |
点评:本题考查了对完全平方公式的应用,注意:完全平方公式有两个:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、形状相同的两个三角形全等 |
| B、能完全重合的两个三角形全等 |
| C、两个等腰直角三角形全等 |
| D、面积相等的两个三角形全等 |
 如图,在△ABC中,D是AB的中点,DE∥BC,若△ADE的面积为3,则△ABC的面积为( )
如图,在△ABC中,D是AB的中点,DE∥BC,若△ADE的面积为3,则△ABC的面积为( )| A、3 | B、6 | C、9 | D、12 |
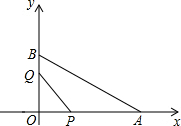 如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么:
如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么: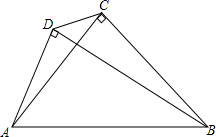 △ABC中,∠ACB=90°,AC=BC,以AB为斜边在△BC的同侧作Rt△ADB,连结CD,探究AD、CD、BD的数量关系.
△ABC中,∠ACB=90°,AC=BC,以AB为斜边在△BC的同侧作Rt△ADB,连结CD,探究AD、CD、BD的数量关系.