题目内容
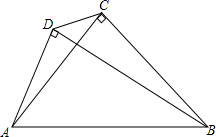 △ABC中,∠ACB=90°,AC=BC,以AB为斜边在△BC的同侧作Rt△ADB,连结CD,探究AD、CD、BD的数量关系.
△ABC中,∠ACB=90°,AC=BC,以AB为斜边在△BC的同侧作Rt△ADB,连结CD,探究AD、CD、BD的数量关系.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:在BD找到一点E使得BE=AD,连接CE,易证△ADC≌△BEC,可得CE=CD,∠BEC=∠ADC,即可求得∠DCE=90°,即可解题.
解答:解:在BD找到一点E使得BE=AD,连接CE,

∵∠DAC+∠CAB+∠ABD=90°,∠CAB+∠ABD+∠CBD=90°,
∴∠DAC=∠CBD,
在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS),
∴CE=CD,∠BEC=∠ADC,
∵∠ADC=∠ADB+∠CDE,∠BEC=∠CDE+∠DCE,
∴∠DCE=∠ADB=90°,
∵CD=CE,
∴DE=
CD,
∴BD=AD+DE=AD+
CD.

∵∠DAC+∠CAB+∠ABD=90°,∠CAB+∠ABD+∠CBD=90°,
∴∠DAC=∠CBD,
在△ADC和△BEC中,
|
∴△ADC≌△BEC(SAS),
∴CE=CD,∠BEC=∠ADC,
∵∠ADC=∠ADB+∠CDE,∠BEC=∠CDE+∠DCE,
∴∠DCE=∠ADB=90°,
∵CD=CE,
∴DE=
| 2 |
∴BD=AD+DE=AD+
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ADC≌△BEC是解题的关键.

练习册系列答案
相关题目
点P(3,2)关于y轴对称点的坐标是( )
| A、(3,-2) |
| B、(-3,2) |
| C、(3,2) |
| D、(-3,-2) |
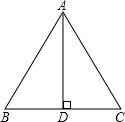 如图,已知AD是△ABC的BC边上的高,补充下列一个条件不能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的BC边上的高,补充下列一个条件不能使△ABD≌△ACD的条件是( )| A、∠B=45° |
| B、BD=CD |
| C、AD平分∠BAC |
| D、AB=AC |
如果-5是一元二次方程x2=c2的一个根,那么常数c是( )
| A、25 | B、±5 | C、5 | D、-25 |
已知A、B、C是同一直线上的三个点,且AB=5cm,BC=4cm,则AC的长为( )
| A、1cm | B、9cm |
| C、1cm或9cm | D、不能确定 |