题目内容
20.计算:(1)$\frac{3}{2+\sqrt{3}}$
(2)$\sqrt{(1-x)^{2}}$+$\sqrt{(2-x)^{2}}$(x≥1)
(3)$\sqrt{\frac{1}{a}+\frac{1}{b}}$(a>0,b>0)
(4)2$\sqrt{\frac{x}{2}}$-$\sqrt{{x}^{3}}$+$\sqrt{8x}$(x>0)
分析 (1)先分母有理化,即可得出答案;
(2)先根据二次根式的性质变形,再去掉绝对值符号,即可得出答案;
(3)先通分,再根据二次根式的性质化成最简即可;
(4)先化成最简根式,再合并即可.
解答 解:(1)原式=$\frac{3×(2-\sqrt{3})}{(2+\sqrt{3})×(2-\sqrt{3})}$
=6-3$\sqrt{3}$;
(2)∵x≥1,
∴①当1≤x≤2时,
原式=|1-x|+|2-x|
=x-1+2-x
=1,
②当x>2时,原式=|1-x|+|2-x|
=x-1+x-2
=2x-3;
(3)∵a>0,b<0,
∴原式=$\sqrt{\frac{a+b}{ab}}$=$\frac{\sqrt{{a}^{2}b+a{b}^{2}}}{ab}$;
(4)∵x>0,
∴原式=$\sqrt{2x}$-x$\sqrt{x}$+2$\sqrt{2x}$=3$\sqrt{2x}$-x$\sqrt{x}$.
点评 本题考查了二次根式的性质,二次根式的混合运算的应用,能正确运用二次根式的运算法则进行化简是解此题的关键,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.己知-2xn-3my3与3x7ym+n是同类项,则mn的值是( )
| A. | 4 | B. | 1 | C. | -4 | D. | -1 |
5.已知反比例函数y=$\frac{k}{x}$的图象经过点P(-3,2),则这个函数的图象位于( )
| A. | 第二、三象限 | B. | 第一、三象限 | C. | 第三、四象限 | D. | 第二、四象限 |
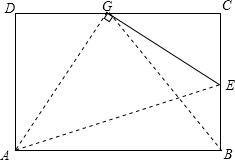 如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长.
如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长.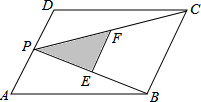 如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )
如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )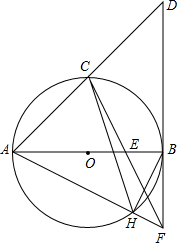 如图,AB是⊙O的直径,点C是$\widehat{AB}$的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,点C是$\widehat{AB}$的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.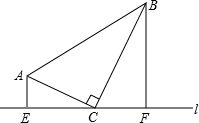 如图,Rt△ABC中,∠ACB=90°,直线l经过C点,AE⊥l交直线l于E点,BF⊥l交直线l于点F,若$\frac{{{S_{△ACE}}}}{{{S_{△CBF}}}}=\frac{4}{9}$,则$\frac{AC}{BC}$=$\frac{2}{3}$.
如图,Rt△ABC中,∠ACB=90°,直线l经过C点,AE⊥l交直线l于E点,BF⊥l交直线l于点F,若$\frac{{{S_{△ACE}}}}{{{S_{△CBF}}}}=\frac{4}{9}$,则$\frac{AC}{BC}$=$\frac{2}{3}$. 如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.
如图,四边形ABCD和四边形AB′C′D都是菱形,且∠BAD=∠B′AD,连接BB′、CC′,BB′与AD相交于点G.