题目内容
1.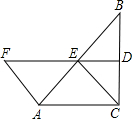 如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,F在DE的延长线上,且AF=CE=AE.
如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,F在DE的延长线上,且AF=CE=AE.(1)求证:四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,AE⊥CF?并说明理由.
分析 (1)由已知条件得出DF∥AC,得出∠AEF=∠EAC,由等腰三角形的性质得出∠AEF=∠F,∠EAC=∠ACE,得出∠AEF=∠F=∠EAC=∠ACE,由AAS证明△AEF≌△EAC,得出EF=AC,即可得出结论;
(2)证明△ACE是等边三角形,得出AC=CE,证出四边形ACEF是菱形,得出对角线互相垂直即可.
解答 (1)证明:∵BC的垂直平分线DE交BC于点D,∠ACB=90°,
∴DF∥AC,
∴∠AEF=∠EAC,
∵AF=CE=AE,
∴∠AEF=∠F,∠EAC=∠ACE,
∴∠AEF=∠F=∠EAC=∠ACE,
在△AEF和△EAC中,
$\left\{\begin{array}{l}{∠F=∠ACE}&{\;}\\{∠AEF=∠EAC}&{\;}\\{AE=EA}&{\;}\end{array}\right.$,
∴△AEF≌△EAC(AAS),
∴EF=AC,
∴四边形ACEF是平行四边形;
(2)解:当∠B=30°时,AE⊥CF;理由如下:
∵∠B=30°,
∴∠EAC=60°,
∴△ACE是等边三角形,
∴AC=CE,
∴四边形ACEF是菱形,
∴AE⊥CF.
点评 本题考查了平行四边形的判定与性质、线段垂直平分线的性质、全等三角形的判定与性质、等边三角形的判定与性质、菱形的判定与性质等知识;本题综合性强,有一定难度.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 已知a、b、c、三数在数轴上对应点如图所示,化简代数式|a|+|b-c|-|ab+1|+|ac-1|-|a+b|.
已知a、b、c、三数在数轴上对应点如图所示,化简代数式|a|+|b-c|-|ab+1|+|ac-1|-|a+b|.