题目内容
12.已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC.

分析 (1)由∠BAC=∠EDF=60°,推出△ABC、△DEF为等边三角形,于是得到∠BCE+∠ACE=∠DCA+∠ECA=60°,推出△BCE≌△ACD(SAS),根据全等三角形的性质得到AD=BE,即可得到结论;
(2)在FA上截取FM=AE,连接DM,推出△AED≌△MFD(SAS),根据全等三角形的性质得到DA=DM=AB=AC,∠ADE=∠MDF,证得∠ADM=∠EDF=∠BAC,推出△ABC≌△DAM(SAS),根据全等三角形的性质得到AM=BC,即可得到结论.
解答 证明:(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF为等边三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,
在△BCE和△ACD中$\left\{\begin{array}{l}BC=AC\\∠BCE=∠ACD\\ CE=CD\end{array}\right.$
∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF;
(2)在FA上截取FM=AE,连接DM,
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
在△AED和△MFD中
$\left\{\begin{array}{l}{AE=MF}\\{∠AKD=∠MFD}\\{KD=FD}\end{array}\right.$
∴△AED≌△MFD(SAS),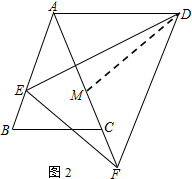
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
在△ABC和△DAM中,$\left\{\begin{array}{l}{AB=DA}\\{∠BAC=∠ADM}\\{AC=DM}\end{array}\right.$,
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,等边三角形的性质,正确的作出辅助线是解题的关键.

| A. | 火车开到月球上 | B. | 抛出的石子会下落 | ||
| C. | 明天临海会下雨 | D. | 早晨的太阳从东方升起 |

 尺规作图:如图,已知线段a,b.
尺规作图:如图,已知线段a,b. (1)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点,求线段MN的长;
(1)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点,求线段MN的长; 如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E.求:
如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E.求: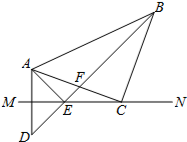 如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.
如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.  如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.