题目内容
3.先化简,再求值:(1-$\frac{1}{x+2}$)÷$\frac{x-1}{x+2}$,其中x=$\sqrt{2}+1$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{x+2-1}{x+2}$•$\frac{x+2}{x-1}$=$\frac{x+1}{x-1}$,
当x=$\sqrt{2}$+1时,原式=$\frac{\sqrt{2}+2}{\sqrt{2}}$=1+$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
12.用配方法把一元二次方程x2+6x+1=0,配成(x+p)2=q的形式,其结果是( )
| A. | (x+3)2=8 | B. | (x-3)2=1 | C. | (x-3)2=10 | D. | (x+3)2=4 |
13.2是-2的( )
| A. | 倒数 | B. | 算术平方根 | C. | 绝对值 | D. | 平方根 |




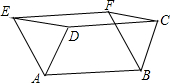 如图,已知?ABCD,以AD、BC为边,在它们的同侧作等边△ADE和等边△BCF,连接EF,求证:四边形ABFE和DCFE都是平行四边形.
如图,已知?ABCD,以AD、BC为边,在它们的同侧作等边△ADE和等边△BCF,连接EF,求证:四边形ABFE和DCFE都是平行四边形.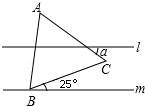 已知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为25°,则∠α的度数为35°.
已知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为25°,则∠α的度数为35°.