题目内容
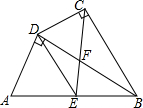 如图,四边形ABCD中,∠ADB=∠DCB=90°,BD平分∠ABC,点E为AB中点.
如图,四边形ABCD中,∠ADB=∠DCB=90°,BD平分∠ABC,点E为AB中点.(1)求证:BD2=BC•BA;
(2)若BD=2
| 6 |
①请直接写出BC的长;
②求
| EF |
| EC |
考点:相似三角形的判定与性质
专题:
分析:(1)证明△CBD∽△BDA即可得到
=
,可得到结论;
(2)①利用(1)的结论,代入可求得BC;②利用角平分线的性质可得
=
,且FC=EC-CF,代入可求得其比值.
| BC |
| BD |
| BD |
| BA |
(2)①利用(1)的结论,代入可求得BC;②利用角平分线的性质可得
| EF |
| FC |
| BE |
| BC |
解答:(1)证明:
∵BD平分∠ABC,C
∴∠CBD=∠DBA,且∠ADB=∠DCB=90°,
∴△CBD∽△BDA,
∴
=
,
∴BD2=BC•BA;
(2)解:
①由(1)可得BD2=BC•BA,且BD=2
,AB=6,
∴(2
)2=6BC,解得BC=4;
②∵BD平分∠ABC,
∴
=
,
∵E为AB中点,
∴BE=
AB=3,
∴
=
,且FC=EC-EF,
∴
=
=
,
∴
=
.
∵BD平分∠ABC,C
∴∠CBD=∠DBA,且∠ADB=∠DCB=90°,
∴△CBD∽△BDA,
∴
| BC |
| BD |
| BD |
| BA |
∴BD2=BC•BA;
(2)解:
①由(1)可得BD2=BC•BA,且BD=2
| 6 |
∴(2
| 6 |
②∵BD平分∠ABC,
∴
| EF |
| FC |
| BE |
| BC |
∵E为AB中点,
∴BE=
| 1 |
| 2 |
∴
| EF |
| FC |
| 3 |
| 4 |
∴
| EF |
| EC-EF |
| 3 |
| 4 |
| 3 |
| 7-3 |
∴
| EF |
| EC |
| 3 |
| 7 |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键.积化比例是解决这类问题的一般思路,在(2)中注意角平分线性质定理的应用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
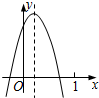 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
 如图,已知线段AB.
如图,已知线段AB. 小王在一块一边靠墙,长为8米,宽为5米的矩形小花园周围栽种了一种花作修饰,如图所示,这块花园的边框宽为30厘米,内外边框所圈的两个矩形相似吗?为什么?
小王在一块一边靠墙,长为8米,宽为5米的矩形小花园周围栽种了一种花作修饰,如图所示,这块花园的边框宽为30厘米,内外边框所圈的两个矩形相似吗?为什么? 如图,△ABC沿DE折叠后,点A落在BC边上的点A′处,且DE∥BC,∠B=50°,则∠BDA′=
如图,△ABC沿DE折叠后,点A落在BC边上的点A′处,且DE∥BC,∠B=50°,则∠BDA′=