题目内容
7.在△ABC中,∠B=30°,点D在BC边上,点E在AC边上,AD=BD,DE=CE,若△ADE为等腰三角形,则∠C的度数为( )| A. | 20° | B. | 20°或30° | C. | 30°或40° | D. | 20°或40° |
分析 先根据三角形外角性质,得出∠ADC=60°,则设∠C=∠EDC=α,进而得到∠ADE=60°-α,∠AED=2α,∠DAE=120°-α,最后根据△ADE为等腰三角形,进行分类讨论即可.
解答 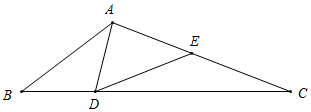 解:如图所示,∵AD=BD,∠B=30°,
解:如图所示,∵AD=BD,∠B=30°,
∴∠ADC=60°,
∵DE=CE,
∴可设∠C=∠EDC=α,则∠ADE=60°-α,∠AED=2α,
根据三角形内角和定理可得,∠DAE=120°-α,
分三种情况:
①当AE=AD时,有60°-α=2α,
解得α=20°;
②当DA=DE时,有120°-α=2α,
解得α=40°;
③当EA=ED时,有120°-α=60°-α,方程无解,
综上所述,∠C的度数为20°或40°,
故选:D.
点评 本题主要考查了等腰三角形的性质,三角形外角性质以及三角形内角和定理的综合应用,解决问题的关键是依据题意画出图形,并进行分类讨论.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
17.下列单项式中正确的是( )
| A. | 单项式-x的次数和系数都是0 | |
| B. | -2016是整式 | |
| C. | -$\frac{{a}^{2}{b}^{\;}}{3}$的系数是-3 | |
| D. | 多项式2x2y3-3x3y3-1是五次三项式 |
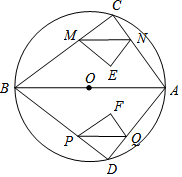 如图,⊙O是△ABC的外接圆,且AB是⊙O的直径,BC=8,AB=10,动点M在线段BC上从点C向点B运动.MN∥AB交AC于点N,四边形CMEN关于MN对称,△ABC与△ABD及四边形CMEN与四边形DPFQ都关于直线AB对称.
如图,⊙O是△ABC的外接圆,且AB是⊙O的直径,BC=8,AB=10,动点M在线段BC上从点C向点B运动.MN∥AB交AC于点N,四边形CMEN关于MN对称,△ABC与△ABD及四边形CMEN与四边形DPFQ都关于直线AB对称.