题目内容
17. 如图:A,B,C三点表示的数分别为a,b,c.
如图:A,B,C三点表示的数分别为a,b,c.利用图形化简:$\left|{\left.{a-b}\right|}\right.-\sqrt{{{({c-b})}^2}}+\sqrt{{{({a-c})}^2}}$=0.
分析 根据数轴判断出a、b、c的正负情况以及绝对值的大小,然后根据绝对值的性质与二次根式的性质化简整理即可.
解答 解:由图可知,a<0,b>0,c<0且|a|<|b|<|c|,
所以,a-b<0,c-b<0,a-c>0,
所以,|a-b|-$\sqrt{(c-b)^{2}}$+$\sqrt{(a-c)^{2}}$=b-a+c-b+a-c=0.
故答案为:0.
点评 本题考查了二次根式的性质与化简,数轴,性质:$\sqrt{{a}^{2}}$=|a|,准确识图判断出a、b、c的正负情况是解题的关键.

练习册系列答案
相关题目
8.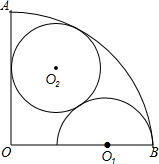 如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
 如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
12. 有理数a、b、c的大小关系如图所示,则下列式子中一定成立的是( )
有理数a、b、c的大小关系如图所示,则下列式子中一定成立的是( )
 有理数a、b、c的大小关系如图所示,则下列式子中一定成立的是( )
有理数a、b、c的大小关系如图所示,则下列式子中一定成立的是( )| A. | a+b+c>0 | B. | |a+b|<c | C. | |a-c|=|a|+c | D. | |b-c|>|c-a| |
9.以下列各线段为边,能组成直角三角形的是( )
| A. | 2,5,8 | B. | 1,1,2 | C. | 4,6,8 | D. | 3,4,5 |

 如图,在Rt△ABC中,已知∠BAC=90°,点D、E、F分别是三边的中点,若AF=3cm,则DE=3cm.
如图,在Rt△ABC中,已知∠BAC=90°,点D、E、F分别是三边的中点,若AF=3cm,则DE=3cm.