题目内容
12.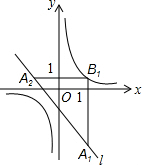 如图,在平面直角坐标系xOy中,已知直线l:t=-x-1,双曲线y=$\frac{1}{x}$.在l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交l于点A2,请继续操作并探究:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,….记点An的横坐标为an,若a1=2,a2015=-$\frac{3}{2}$.
如图,在平面直角坐标系xOy中,已知直线l:t=-x-1,双曲线y=$\frac{1}{x}$.在l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交l于点A2,请继续操作并探究:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,….记点An的横坐标为an,若a1=2,a2015=-$\frac{3}{2}$.
分析 首先根据a1=2,求出a2,a3,a4,a5的值,总结出其中的规律:每3个数为一个循环;然后用2015除以3,根据商和余数的情况,判断出a2015的值是多少即可.
解答 解:解:当a1=2时,B1的纵坐标为$\frac{1}{2}$,
∵B1的纵坐标和A2的纵坐标相同,
∴A2的横坐标为a2=-1-$\frac{1}{2}$=-$\frac{3}{2}$,
∵A2的横坐标和B2的横坐标相同,
∴B2的纵坐标为b2=$\frac{1}{-\frac{3}{2}}$=-$\frac{2}{3}$,
∵B2的纵坐标和A3的纵坐标相同,
∴A3的横坐标为a3=-1-(-$\frac{2}{3}$)=-$\frac{1}{3}$,
∵A3的横坐标和B3的横坐标相同,
∴B3的纵坐标为b3=$\frac{1}{-\frac{1}{3}}$=-3,
∵B3的纵坐标和A4的纵坐标相同,
∴A4的横坐标为a4=-1-(-3)=2,
∵A4的横坐标和B4的横坐标相同,
∴B4的纵坐标为b4=$\frac{1}{2}$,
∴a1,a2,a3,a4,…,每3个数一个循环,分别是2、-$\frac{3}{2}$、-$\frac{1}{3}$,
∵2015÷3=671…2,
∴a2015是第672个循环的第2个数,
∴a2015=-$\frac{3}{2}$.
故答案为:$-\frac{3}{2}$.
点评 此题主要考查了反比例函数图象上点的坐标的特征,要熟练掌握,解答此题的关键是要明确:①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
3.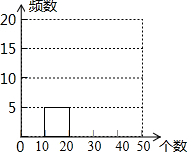 体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
(1)表中a=9;
(2)补全频数分布直方图;
(3)求第四组点球各所在40≤x<50的人数占被调查人数的百分比;
(4)若垫球个数在20个以上(含20个)算合格,该校七年级有400名学生,请你估计该校七年级学生在这一项目中合格的学生约有多少人?
 体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.| 组别 | 垫球个数x(个) | 频数(人数) |
| 1 | 10≤x<20 | 5 |
| 2 | 20≤x<30 | a |
| 3 | 30≤x<40 | 20 |
| 4 | 40≤x<50 | 16 |
(2)补全频数分布直方图;
(3)求第四组点球各所在40≤x<50的人数占被调查人数的百分比;
(4)若垫球个数在20个以上(含20个)算合格,该校七年级有400名学生,请你估计该校七年级学生在这一项目中合格的学生约有多少人?
4.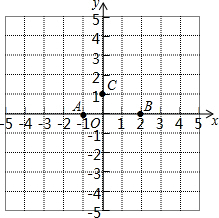 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
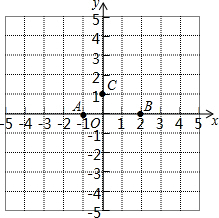 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )| A. | (3,1) | B. | (-4,1) | C. | (1,-1) | D. | (-3,1) |
2.下列各组数中,不是x+y=7的解是( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=10}\\{y=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=12}\\{y=-1}\end{array}\right.$ |
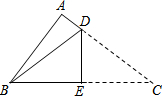 如图,在△ABC中,∠A=90°,AB=6,BC=10,现将△ABC沿折痕DE进行折叠,使顶点C、B重合,则△ABD的周长等于14.
如图,在△ABC中,∠A=90°,AB=6,BC=10,现将△ABC沿折痕DE进行折叠,使顶点C、B重合,则△ABD的周长等于14. 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=5.则矩形的对角线长是( )
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=5.则矩形的对角线长是( ) 如图,已知,在直角三角形ABC中,∠A=90°,AB=3,AC=4,BC=5,则顶点A到BC边的距离等于2.4.
如图,已知,在直角三角形ABC中,∠A=90°,AB=3,AC=4,BC=5,则顶点A到BC边的距离等于2.4.