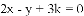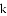题目内容
阅读下列材料并解答问题：
“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”
数学兴趣小组探究得到如下解法：
因为x-y=2，
所以x=y+2.
因为x＞1，
所以y+2＞1.
因为y＜0，
所以-1＜y＜0. ①
同理得1＜x＜2. ②
有①+ ②得-1+1＜x+y＜0+2，
所以x+y的取值范围是0＜x+y＜2.
请按照上述方法，完成下列问题：
（1）已知x﹣y=3，且x＞2，y＜1，试确定x+y的取值范围．
（2）已知y＞1，x＜﹣1，若x﹣y=a成立，直接写出x+y的取值范围（结果用含a的式子表示）______________．
练习册系列答案
相关题目
）÷（
）转化为乘法是（ ）
B. （
中，自变量
某体育用品商店一天中卖出某种品牌的运动鞋15双，其中各种尺码的鞋的销售量如表所示：
鞋的尺码/cm | 23 | 23.5 | 24 | 24.5 | 25 |
销售量/双 | 1 | 3 | 3 | 6 | 2 |
则这15双鞋的尺码组成的一组数据中，众数和中位数分别为（ ）
A. 24.5，24.5 B. 24.5，24 C. 24，24 D. 23.5，24
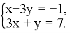
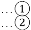
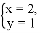是方程
