题目内容
20. 如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于D.
如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于D.(1)求证:△ADE∽△ABC;
(2)连结DE,如果DE=1,BC=3,求MN的长.
分析 (1)根据MN∥BC,得到$\frac{AM}{BC}=\frac{AD}{BD}$,$\frac{AN}{BC}=\frac{AE}{CE}$,等量代换得到$\frac{AD}{BD}=\frac{AE}{EC}$,根据相似三角形的判定即可得到结论;
(2)根据$\frac{AD}{BD}=\frac{AE}{EC}$,得到DE∥BC,根据平行线分线段成比例定理得到$\frac{AD}{AB}=\frac{DE}{BC}=\frac{1}{3}$,于是推出$\frac{AD}{BD}=\frac{1}{2}$,即$\frac{AM}{BC}=\frac{AD}{BD}=\frac{1}{2}$,即可得到结论.
解答 (1)证明:∵MN∥BC,
∴$\frac{AM}{BC}=\frac{AD}{BD}$,$\frac{AN}{BC}=\frac{AE}{CE}$,
又∵AM=AN,
∴$\frac{AD}{BD}=\frac{AE}{EC}$,
∴△ADE∽△ABC;
(2)解:∵$\frac{AD}{BD}=\frac{AE}{EC}$,
∴DE∥BC,
∴$\frac{AD}{AB}=\frac{DE}{BC}=\frac{1}{3}$,
∴$\frac{AD}{BD}=\frac{1}{2}$,即$\frac{AM}{BC}=\frac{AD}{BD}=\frac{1}{2}$,
∴AM=$\frac{1}{2}$BC=$\frac{3}{2}$,
∴MN=2AM=3.
点评 本题考查了相似三角形的判定和性质,平行线分线段成比例,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
17.将边长为1的正方形纸片如图1所示的方法进行对折,记第一次对折后得到的图形面积为 S1,第2次对折后得到的图形面积为S2…,第n次对折后得到的图形面积为Sn,请根据图2化简S1+S2+S3…S2014=( )
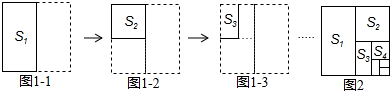

| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
8. 如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
 如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )
如图是一张关于340万年前地球表层的照片,340万用科学记数法表示为( )| A. | 3.40×102 | B. | 340×104 | C. | 3.40×104 | D. | 3.40×106 |
10.已知二次函数y=ax2+bx+c(a≠0)的图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
求:
(1)这个二次函数的解析式;
(2)这个二次函数图象的顶点坐标及上表中m的值.
| x | … | -1 | 0 | 2 | 4 | … |
| y | … | -5 | 1 | 1 | m | … |
(1)这个二次函数的解析式;
(2)这个二次函数图象的顶点坐标及上表中m的值.
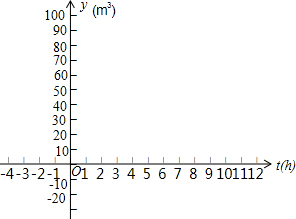 某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.
某水池的容积为90m3,水池中已有水10m3,现按8m3/h的流量向水池中注水.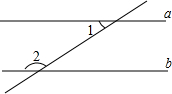 已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.
已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b. 中秋节期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成三个面积相等的扇形,三个扇形区域里分别标有“10元”、“20元”、“30元”的字样(如图).规定:同一天内,顾客在本商场每消费满100元,就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券.某顾客当天消费240元,转了两次转盘.
中秋节期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成三个面积相等的扇形,三个扇形区域里分别标有“10元”、“20元”、“30元”的字样(如图).规定:同一天内,顾客在本商场每消费满100元,就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券.某顾客当天消费240元,转了两次转盘.