题目内容
1.若xyz≠0,并且满足3x=7y=63z,则$\frac{{x}^{2}{y}^{2}-4xy{z}^{2}-{x}^{2}{z}^{2}}{{y}^{2}{z}^{2}}$=4.分析 先根据3x=7y=63z,得出3x•7y=34z×72z,进而得到x=4z,y=2z,最后代入代数式进行化简计算即可.
解答 解:∵3x=7y=63z,
∴3x•7y=(63z)2,
又∵(63z)2=632z=(32×7)2z=34z×72z,
∴3x•7y=34z×72z,
即x=4z,y=2z,
∴$\frac{{x}^{2}{y}^{2}-4xy{z}^{2}-{x}^{2}{z}^{2}}{{y}^{2}{z}^{2}}$=$\frac{(4z)^{2}•(2z)^{2}-4×4z×2z-(4z)^{2}•{z}^{2}}{(2z)^{2}•{z}^{2}}$=$\frac{16{z}^{4}}{4{z}^{4}}$=4.
故答案为:4.
点评 本题主要考查了分式求值问题,解决问题的关键是从已知条件和所求问题的特点出发,通过适当的变形、转化,才能发现解题的捷径.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
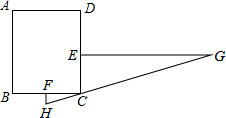 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长 9 里,城墙BC长 7 里,东门所在的点E,南门所在的点F分别是CD,BC 的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=1.05里.
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长 9 里,城墙BC长 7 里,东门所在的点E,南门所在的点F分别是CD,BC 的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=1.05里. 如图,AD=AE,∠1=∠2,试说明:BE=CD.
如图,AD=AE,∠1=∠2,试说明:BE=CD. 如图,已知AB=AC,CE⊥AB,BF⊥AC.求证:BF=CE.
如图,已知AB=AC,CE⊥AB,BF⊥AC.求证:BF=CE.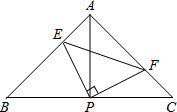 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边 PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合).现给出以下四个结论: