题目内容
8.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=4,BC=9,AD=6,点E,F分别在边AD,BC上,且BF=2DE,联结FE,FE的延长线于CD的延长线相交于点P,设DE=x,$\frac{PE}{EF}$=y.(1)求y关于x的函数解析式,并写出函数的定义域;
(2)当以ED为半径的⊙E与以FB为半径的⊙F外切时,求x的值;
(3)当△AEF∽△PED时,求x的值.
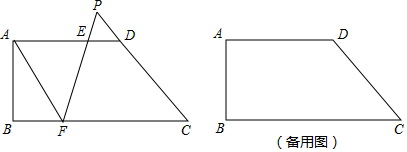
分析 (1)根据已知条件得到BF=2x,CF=9-2x,根据相似三角形的性质即可的结论;
(2)根据相切两圆的性质得到x+2x=EF,过E作EG⊥BC于G,根据勾股定理即可得到结论;
(3)①当∠EAF=∠EDP时,有$\frac{DE}{EA}=\frac{PE}{EF}$,于是得到结论;②当∠EFA=∠EDP时,过E作EG∥PC交BC于G,根据相似三角形的性质即可得到结论.
解答 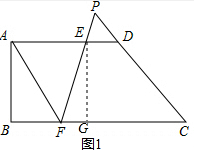 解:(1)∵BF=2DE,DE=x,
解:(1)∵BF=2DE,DE=x,
∴BF=2x,
∵BC=9,
∴CF=9-2x,
∵AD∥BC,
∴△PDE∽△PCF,
∴$\frac{PE}{PF}=\frac{DE}{CF}$,
∵$\frac{PE}{EF}$=y,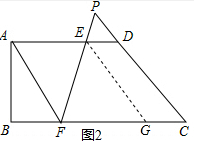
∴y=$\frac{DE}{CF-DE}=\frac{x}{9-3x}$,
∴y=$\frac{x}{9-3x}$(0<x<3);
(2)∵⊙E的半径=x,⊙F的半径=2x,
∵以ED为半径的⊙E与以FB为半径的⊙F外切,
∴x+2x=EF,
过E作EG⊥BC于G,
∴EG=AB=4,FG=6-3x,
∴EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=$\sqrt{{4}^{2}+(6-3x)^{2}}$,
∴x+2x=$\sqrt{{4}^{2}+(6-3x)^{2}}$,
解得x=$\frac{13}{9}$;
(3)当△AEF∽△PED时,
①当∠EAF=∠EDP时,有$\frac{DE}{EA}=\frac{PE}{EF}$,
即$\frac{x}{6-x}=\frac{x}{9-3x}$,
解得:x=$\frac{3}{2}$;
②当∠EFA=∠EDP时,过E作EG∥PC交BC于G,
则CG=ED=x,EG=9-3x,
∵△EFA∽△FGE,
∴$\frac{EF}{FG}=\frac{EA}{FE}$,
∴EF2=FG•EA,即42+(6-3x)2=(9-3x)(6-x),
∴x=$\frac{9+\sqrt{129}}{12}$.
点评 本题考查了相似三角形的判定和性质,平行线的性质,勾股定理,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 10、5、4 | B. | 3、4、2 | C. | 1、11、8 | D. | 5、3、8 |
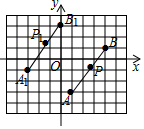 如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )| A. | (a-4,b+2) | B. | (a-4,b-2) | C. | (a+4,b+2) | D. | (a+4,b-2) |
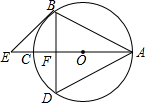 如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点
如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点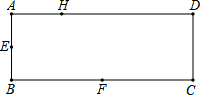 如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( )
如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( )