题目内容
19.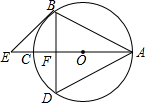 如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点
如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点(1)求证:BE为⊙O的切线;
(2)若AF=4CF,求tan∠E.
分析 (1)连接CD、OD、BO,延长BO交AD于点G,证△ABO≌△DBO得∠1=∠ABO,从而得BG⊥AD,即∠1+∠2=90°,根据∠2=∠3知∠3+∠1=90°,得证;
(2)设CF=x,则AF=4x、OC=OB=$\frac{1}{2}$AC=$\frac{5}{2}$x、OF=OC-CF=$\frac{3}{2}$x,证△CDF∽△OBF得$\frac{CD}{OB}$=$\frac{CF}{OF}$,从而求得CD=$\frac{5}{3}$x、AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\frac{10\sqrt{2}}{3}$x,由tanE=tan∠CAD=$\frac{CD}{AD}$可得答案.
解答 解:(1)如图,连接CD、OD、BO,延长BO交AD于点G,
在△ABO和△DBO中,
∵$\left\{\begin{array}{l}{AB=DB}\\{BO=BO}\\{AO=DO}\end{array}\right.$,
∴△ABO≌△DBO(SSS),
∴∠1=∠ABO,
∴BG⊥AD,
∴∠1+∠2=90°,
∵BE∥AD,
∴∠2=∠3,
∴∠3+∠1=90°,即OB⊥BE,
∴BE为⊙O的切线;
(2)设CF=x,则AF=4x,
∴AC=5x,OC=OB=$\frac{1}{2}$AC=$\frac{5}{2}$x,
∴OF=OC-CF=$\frac{5}{2}$x-x=$\frac{3}{2}$x,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴CD∥BG,
∴△CDF∽△OBF,
∴$\frac{CD}{OB}$=$\frac{CF}{OF}$,即$\frac{CD}{\frac{5}{2}x}$=$\frac{x}{\frac{3}{2}x}$,
则CD=$\frac{5}{3}$x,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{(5x)^{2}-(\frac{5}{3}x)^{2}}$=$\frac{10\sqrt{2}}{3}$x,
∵BE∥AD,
∴tanE=tan∠CAD=$\frac{CD}{AD}$=$\frac{\frac{5}{3}x}{\frac{10\sqrt{2}}{3}x}$=$\frac{\sqrt{2}}{4}$.
点评 本题考查了切线的判定、平行线的性质、相似三角形的判定与性质、全等三角形的判定和性质,正确的作出辅助线是解题的关键.

 如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )
如图,D是等边△ABC外接圆上的点,且∠DAC=20°,则∠ACD的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 45° |
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 平分弦的直径垂直弦 | |
| C. | 有两边及一角对应相等的两个三角形全等 | |
| D. | 八边形的内角和是外角和的3倍 |
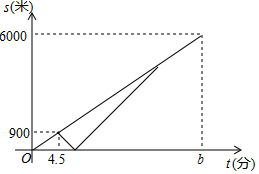 周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园,两人同时从学校出发,以a米/分的速度匀速行驶,出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙,甲追上乙后,两人以相同的速度前往净月潭,乙骑自行车的速度始终不变,设甲,乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园,两人同时从学校出发,以a米/分的速度匀速行驶,出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙,甲追上乙后,两人以相同的速度前往净月潭,乙骑自行车的速度始终不变,设甲,乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.