题目内容
12.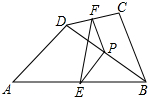 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )| A. | 120° | B. | 150° | C. | 135° | D. | 140° |
分析 根据中位线定理和已知,易证明△EPF是等腰三角形,由等腰三角形的性质即可求出∠EPF的度数.
解答 解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF=$\frac{1}{2}$BC,PE=$\frac{1}{2}$AD,
∵AD=BC,
∴PF=PE,
故△EPF是等腰三角形.
∵∠PEF=30°,
∴∠PEF=∠PFE=30°,
∴∠EPF=120°.
故选A.
点评 本题考查了三角形中位线定理及等腰三角形的性质,解题时要善于根据已知信息,确定应用的知识是解题关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
4.下列调查中,适宜采用全面调查方式的是( )
| A. | 调查春节联欢晚会在武汉市的收视率 | |
| B. | 了解全班同学参加社会实践活动的情况 | |
| C. | 调查某品牌食品的色素含量是否达标 | |
| D. | 了解一批手机电池的使用寿命 |
1.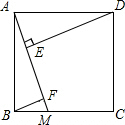 如图,正方形ABCD的边长为5,点M是边BC上的点,DE⊥AM于点E,BF∥DE,交AM于点F.若E是AF的中点,则DE的长为( )
如图,正方形ABCD的边长为5,点M是边BC上的点,DE⊥AM于点E,BF∥DE,交AM于点F.若E是AF的中点,则DE的长为( )
 如图,正方形ABCD的边长为5,点M是边BC上的点,DE⊥AM于点E,BF∥DE,交AM于点F.若E是AF的中点,则DE的长为( )
如图,正方形ABCD的边长为5,点M是边BC上的点,DE⊥AM于点E,BF∥DE,交AM于点F.若E是AF的中点,则DE的长为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 2$\sqrt{3}$ |
2. 如图,若AD∥BC,那么( )
如图,若AD∥BC,那么( )
 如图,若AD∥BC,那么( )
如图,若AD∥BC,那么( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠B=∠D | D. | ∠B=∠3 |
 你能利用如图验证勾股定理吗?
你能利用如图验证勾股定理吗?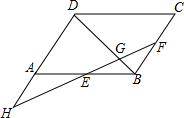 如图所示,在?ABCD中,E为AB中点,在BC上取一点F,使BF:FC=1:2,连接EF交DA的延长线于H,交BD于G.试说明:BD=5BG.
如图所示,在?ABCD中,E为AB中点,在BC上取一点F,使BF:FC=1:2,连接EF交DA的延长线于H,交BD于G.试说明:BD=5BG. 如图,将长方形ABCD沿AE折叠,若∠BAD′比∠D′AE大15°,则∠D′AE=25度.
如图,将长方形ABCD沿AE折叠,若∠BAD′比∠D′AE大15°,则∠D′AE=25度. 如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗?
如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗? 如图,在△ABC中,∠CAB=90°,点D、E、F分别是BC、AC、AB的中点,连结EF,AD.求证:EF=AD.
如图,在△ABC中,∠CAB=90°,点D、E、F分别是BC、AC、AB的中点,连结EF,AD.求证:EF=AD.