题目内容
2. 你能利用如图验证勾股定理吗?
你能利用如图验证勾股定理吗?
分析 直角梯形的面积由三部分组成,利用直角梯形的面积等于三个直角三角形的面积之和列出方程并整理即可证明勾股定理.
解答 证明:梯形的面积,可以写成:$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(a+b)2;
也可以写成:$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2.
∴$\frac{1}{2}$(a+b)2=$\frac{1}{2}$ab+$\frac{1}{2}$ab+c2;
∴a2+b2=c2.
点评 本题考查了勾股定理的证明.此类证明要转化成该图形面积的两种表示方法,从而转化成方程达到证明的结果.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.已知直角三角形两边的长为6和8,则此三角形的周长为( )
| A. | 24 | B. | 14+2$\sqrt{7}$ | C. | 24或14+2$\sqrt{7}$ | D. | 以上都不对 |
7.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
| A. | AD=BC,AB=DC | B. | OA=OC,OB=OD | C. | AB∥DC,AD=BC | D. | ∠A=∠C,∠B=∠D |
12.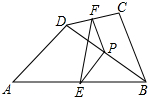 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )| A. | 120° | B. | 150° | C. | 135° | D. | 140° |
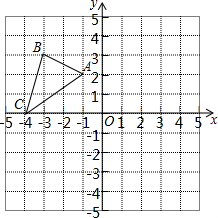 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.