题目内容
7. 如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗?
如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗?
分析 首先根据EB∥MF可得∠BEM=∠FME,然后证明△BDE≌△FDM可得BE=MF.
解答 解:∵BE∥MF,
∴∠E=∠DMF,
在△BDE和△FDM中,
$\left\{\begin{array}{l}{DB=DF}\\{∠BDE=∠MDF}\\{∠E=∠DMF}\end{array}\right.$,
∴△BDE≌△FDM(AAS),
∴BE=MF.
点评 此题主要考查了全等三角形的应用,关键是正确证明△BDE≌△FDM.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
12.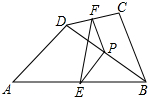 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )| A. | 120° | B. | 150° | C. | 135° | D. | 140° |
 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,求AC的长.
如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,求AC的长.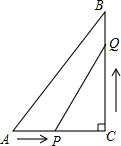 如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.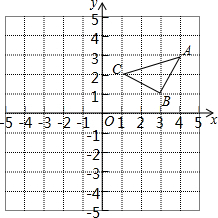 如图所示的平面直角坐标系中,将△ABC平移后得到△DEF.已知B点平移的对应点E点(0,-3)(A点与D点对应,C点与F点对应).
如图所示的平面直角坐标系中,将△ABC平移后得到△DEF.已知B点平移的对应点E点(0,-3)(A点与D点对应,C点与F点对应).