题目内容
17. 如图,在△ABC中,∠CAB=90°,点D、E、F分别是BC、AC、AB的中点,连结EF,AD.求证:EF=AD.
如图,在△ABC中,∠CAB=90°,点D、E、F分别是BC、AC、AB的中点,连结EF,AD.求证:EF=AD.
分析 由DE,DF是△ABC的中位线,可得四边形EAFD是平行四边形,又∠CAB=90°,可知四边形EAFD是矩形,根据矩形对角线相等即可得证.
解答 证明:∵点D、E、F分别是BC、AC、AB的中点,
∴DE,DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形EAFD是平行四边形,
∵∠CAB=90°,
∴四边形EAFD是矩形,
∴EF=AD.
点评 本题主要考查了矩形的判定和性质以及三角形中位线,掌握三角形中位线平行第三边且等于第三边的一半和能够证明四边形EAFD是矩形是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
7.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
| A. | AD=BC,AB=DC | B. | OA=OC,OB=OD | C. | AB∥DC,AD=BC | D. | ∠A=∠C,∠B=∠D |
5.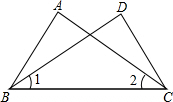 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠ABC=∠DBC |
12.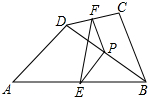 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )| A. | 120° | B. | 150° | C. | 135° | D. | 140° |
9.从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.设从甲地到乙地上坡与平路分别为x km,y km,依题意,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{5}+\frac{y}{4}=\frac{42}{60}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{4}+\frac{y}{5}=\frac{42}{60}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{5}+\frac{y}{4}=42}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{4}+\frac{y}{5}=42}\end{array}\right.$ |
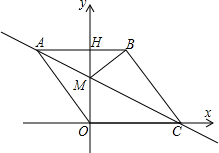 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
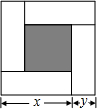 如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个相同长方形的两边长(x>y),给出以下关系式:①x+y=m;②x-y=n;③xy=$\frac{{m}^{2}-{n}^{2}}{4}$. 其中正确的关系式的个数有( )
如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个相同长方形的两边长(x>y),给出以下关系式:①x+y=m;②x-y=n;③xy=$\frac{{m}^{2}-{n}^{2}}{4}$. 其中正确的关系式的个数有( )