题目内容
20. 如图,将长方形ABCD沿AE折叠,若∠BAD′比∠D′AE大15°,则∠D′AE=25度.
如图,将长方形ABCD沿AE折叠,若∠BAD′比∠D′AE大15°,则∠D′AE=25度.
分析 设∠D′AE=x°,则∠DAE=∠D′AE=x°,∠BAD′=(x+15)°,根据矩形的性质得出x+x+x+15=90,求出即可.
解答 解:设∠D′AE=x°,则∠DAE=∠D′AE=x°,∠BAD′=(x+15)°,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴x+x+x+15=90,
解得:x=25°,
即∠D′AE=25°.
故答案为:25.
点评 本题考查了折叠的性质,矩形的性质的应用,能得出关于x的方程是解此题的关键,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知直角三角形两边的长为6和8,则此三角形的周长为( )
| A. | 24 | B. | 14+2$\sqrt{7}$ | C. | 24或14+2$\sqrt{7}$ | D. | 以上都不对 |
5.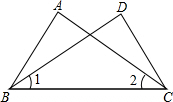 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠ABC=∠DBC |
12.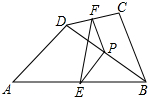 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )| A. | 120° | B. | 150° | C. | 135° | D. | 140° |
9.从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.设从甲地到乙地上坡与平路分别为x km,y km,依题意,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{5}+\frac{y}{4}=\frac{42}{60}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{4}+\frac{y}{5}=\frac{42}{60}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{5}+\frac{y}{4}=42}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{4}+\frac{y}{5}=42}\end{array}\right.$ |
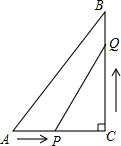 如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.