题目内容
1.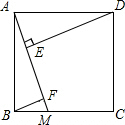 如图,正方形ABCD的边长为5,点M是边BC上的点,DE⊥AM于点E,BF∥DE,交AM于点F.若E是AF的中点,则DE的长为( )
如图,正方形ABCD的边长为5,点M是边BC上的点,DE⊥AM于点E,BF∥DE,交AM于点F.若E是AF的中点,则DE的长为( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 2$\sqrt{3}$ |
分析 因为AF=AE+EF,则可以通过证明△ABF≌△DAE,从而得到AE=BF,便得到了AF=BF+EF,再利用勾股定理求出DE的长即可.
解答 证明:∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°
∵DE⊥AG,
∴∠DEM=∠AED=90°
∴∠ADE+∠DAE=90°
又∵∠BAF+∠DAE=∠BAD=90°,
∴∠ADE=∠BAF.
∵BF∥DE,
∴∠AFB=∠DEG=∠AED.
在△ABF与△DAE中,
$\left\{\begin{array}{l}{∠AFB=∠AED}\\{∠ADE=∠BAF}\\{AD=AB}\end{array}\right.$,
∴△ABF≌△DAE(AAS).
∴BF=AE,
∵BF∥DE,∠AED=90°
∴∠AFB=90°,
∵E是AF的中点,
∴AE=EF,
又∵BF=AE,
∴BF=EF=AE,
设BF为x,则AF为2x,
∵AB2=AF2+BF2,
∴52=(2x)2+x2,
解得x=$±\sqrt{5}$(舍去$-\sqrt{5}$),
∴AF=2x=$2\sqrt{5}$,
∵DE=AF,
∴DE=$2\sqrt{5}$,
故选:B.
点评 此题主要考查学生对正方形的性质及全等三角形的判定的掌握情况,解题的关键是熟练掌握全等三角形的判定方法以及正方形的各种有关性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.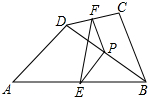 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )| A. | 120° | B. | 150° | C. | 135° | D. | 140° |
9.从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.设从甲地到乙地上坡与平路分别为x km,y km,依题意,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{5}+\frac{y}{4}=\frac{42}{60}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=\frac{54}{60}}\\{\frac{x}{4}+\frac{y}{5}=\frac{42}{60}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{5}+\frac{y}{4}=42}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=54}\\{\frac{x}{4}+\frac{y}{5}=42}\end{array}\right.$ |
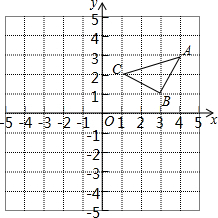 如图所示的平面直角坐标系中,将△ABC平移后得到△DEF.已知B点平移的对应点E点(0,-3)(A点与D点对应,C点与F点对应).
如图所示的平面直角坐标系中,将△ABC平移后得到△DEF.已知B点平移的对应点E点(0,-3)(A点与D点对应,C点与F点对应).