题目内容
14. 如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )| A. | 100° | B. | 72° | C. | 64° | D. | 36° |
分析 连接OA,根据等腰三角形的性质得到∠OAC=∠C=28°,根据等腰三角形的性质解答即可.
解答 解: 连接OA,
连接OA,
∵OA=OC,
∴∠OAC=∠C=28°,
∴∠OAB=64°,
∵OA=OB,
∴∠B=∠OAB=64°,
故选:C.
点评 本题考查的是圆周角定理,掌握圆的半径相等、等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
4.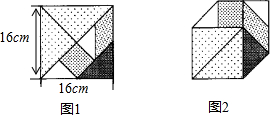 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
9.已知A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=$\frac{2}{x}$上的三点,若x1<x2<x3,y2<y1<y3,则下列关系式不正确的是( )
| A. | x1•x2<0 | B. | x1•x3<0 | C. | x2•x3<0 | D. | x1+x2<0 |
6.如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )


| A. | 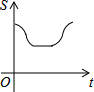 | B. | 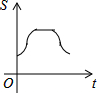 | C. | 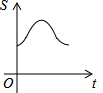 | D. |  |
3.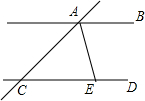 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )| A. | 40° | B. | 70° | C. | 80° | D. | 140° |
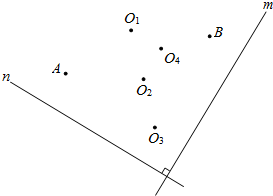 如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )
如图,直线m⊥n,在某平面直角坐标系中,x轴∥m,y轴∥n,点A的坐标为(-4,2),点B的坐标为(2,-4),则坐标原点为( )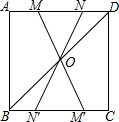 如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( ) 如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.