题目内容
4.已知x=$\root{3}{4(\sqrt{5}+1)}$-$\root{3}{4(\sqrt{5}-1)}$,则x3+12x的算术平方根是( )| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 观察题目,可借助于整体思想,设$\root{3}{\sqrt{5}+1}$=a,$\root{3}{\sqrt{5}-1}$=b,进行替换,加以解答.
解答 解:设$\root{3}{\sqrt{5}+1}$=a,$\root{3}{\sqrt{5}-1}$=b,则a3=$\sqrt{5}$+1,b3=$\sqrt{5}$-1.
又∵4=($\sqrt{5}$+1)($\sqrt{5}$-1)=a3b3,
∴x=a2b-ab2,x2=a4b2-2a3b3+a2b4,
故原式=x(x2+12)
=(a2b-ab2)(a4b2-2a3b3+a2b4+12)
=(a2b-ab2)(a4b2-8+a2b4+12)
=(a2b-ab2)(a4b2+a2b4+4)
=ab(a-b)a2b2(a2+b2+ab)
=a3b3(a3-b3)
=($\sqrt{5}$+1)($\sqrt{5}$-1)($\sqrt{5}$+1-$\sqrt{5}$+1)
=4×2
=8.
则其算术平方根是:2$\sqrt{2}$.
故选:D.
点评 此题主要考查了立方根、算术平方根的定义,解题时注意运用公式简便计算(a+b)(a-b)=a2-b2;(a-b)(a2+ab+b2)=a3-b3.同时注意用一个字母可以表示一个较复杂的数的整体思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.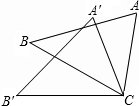 如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
 如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
12.已知等边三角形的面积为$\sqrt{3}$,则它的高等于( )
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $2\sqrt{6}$ | D. | 4 |
14.下列说法中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 64的立方根是±4 | ||
| C. | 6的平方根是$\sqrt{6}$ | D. | 0.01的算术平方根是0.1 |
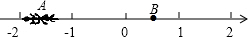 如图,一只蚂蚁从A点沿数轴向右爬行2个单位长度到达点B,点A表示的数是-$\sqrt{2}$,设点B表示的数是m.
如图,一只蚂蚁从A点沿数轴向右爬行2个单位长度到达点B,点A表示的数是-$\sqrt{2}$,设点B表示的数是m. 已知:如图,E是等腰三角形ABC的腰AC上的任意一点,ED⊥BC,垂足为D,延长DE交BA的延长线于点F.求证:点A在EF的垂直平分线上.
已知:如图,E是等腰三角形ABC的腰AC上的任意一点,ED⊥BC,垂足为D,延长DE交BA的延长线于点F.求证:点A在EF的垂直平分线上.