题目内容
15.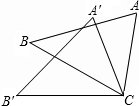 如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
分析 根据全等三角形的性质得出∠A′CB′=∠ACB,求出∠B′CB=∠ACA′,代入=∠BCB′=∠A′CB′-∠A′CB求出即可.
解答 解:∵△ACB≌△A′CB′,
∴∠A′CB′=∠ACB,
∴∠A′CB′-∠A′CB=∠ACB-∠A′CB,
∴∠B′CB=∠ACA′,
∵∠A′CB′=65°,∠A′CB=35°,
∴∠ACA′=∠BCB′=∠A′CB′-∠A′CB=65°-35°=30°,
故选B.
点评 本题考查了全等三角形的性质的应用,解此题的关键是求出∠B′CB=∠ACA′,注意:全等三角形的对应角相等,难度适中.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
4.已知x=$\root{3}{4(\sqrt{5}+1)}$-$\root{3}{4(\sqrt{5}-1)}$,则x3+12x的算术平方根是( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
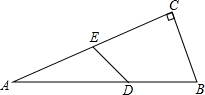 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,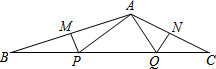 如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于80°.
如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于80°.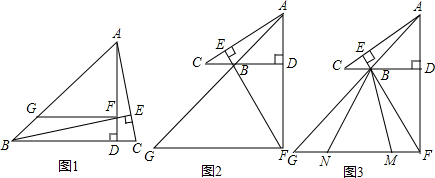
 一个几何体的三视图如图所示,分别求出这个几何体的体积和表面积.
一个几何体的三视图如图所示,分别求出这个几何体的体积和表面积.