题目内容
12.已知等边三角形的面积为$\sqrt{3}$,则它的高等于( )| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $2\sqrt{6}$ | D. | 4 |
分析 根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可根据三角形ABC的面积,即可解题.
解答 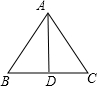 解:等边三角形高线即中线,故D为BC中点,
解:等边三角形高线即中线,故D为BC中点,
设BC=a,
∴BD=$\frac{1}{2}$a,AD=$\frac{\sqrt{3}}{2}$a
∴等边△ABC的面积=$\frac{1}{2}$BC•AD=$\sqrt{3}$,
∴$\frac{1}{2}$×a×$\frac{\sqrt{3}}{2}$a=$\sqrt{3}$,
解得a=2.
∴AD=$\frac{\sqrt{3}}{2}$a=$\sqrt{3}$
故选A.
点评 本题考查了等边三角形的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理计算AD的值是解题的关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
4.已知x=$\root{3}{4(\sqrt{5}+1)}$-$\root{3}{4(\sqrt{5}-1)}$,则x3+12x的算术平方根是( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
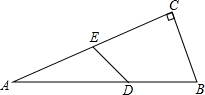 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6,