题目内容
16.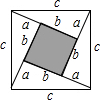 如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.
如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.
分析 根据勾股定理得出a2+b2=c2,求出(a+b)2-2ab=c2,把a+b=4和c=3代入求出ab的值,即可求出答案.
解答 解:∵a2+b2=c2,
∴(a+b)2-2ab=c2,
又∵a+b=4,斜边c长为3,
∴42-2ab=32,
∴ab=$\frac{7}{2}$,
∴直角三角形的面积为$\frac{1}{2}$ab=$\frac{7}{4}$,
故答案为:$\frac{7}{4}$.
点评 本题考查了完全平方公式和勾股定理的应用,能根据公式和定理求出ab的值是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的( )| A. | abc>0 | |
| B. | 9a+3b+c>0 | |
| C. | a+b≥m(am+b)(m≠1的实数) | |
| D. | 方程ax2+bx+c=2有两个不相等的实数根 |
11.如果点P在x轴正半轴上,则点P的坐标为( )
| A. | (0,2) | B. | (-2,0) | C. | (4,0) | D. | (0,-1) |

 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A2015的坐标为(504,504).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A2015的坐标为(504,504).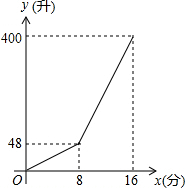 一个容积为400升的水箱,安装有A、B两个注水管,注水过程中A水管始终打开,B水管8分钟后打开,两水管的注水速度均为定值.当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A水管注水时间时间x(分)之间的函数图象如图所示.
一个容积为400升的水箱,安装有A、B两个注水管,注水过程中A水管始终打开,B水管8分钟后打开,两水管的注水速度均为定值.当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A水管注水时间时间x(分)之间的函数图象如图所示.